Inference-Time Scaling for Diffusion Models beyond Scaling Denoising Steps

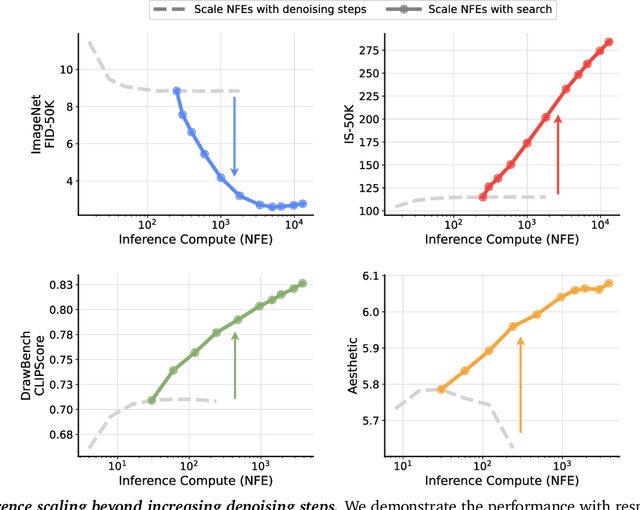
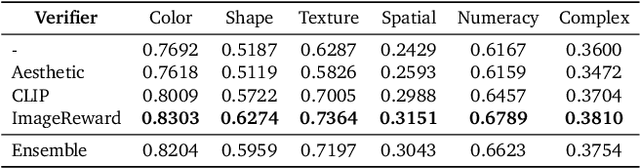
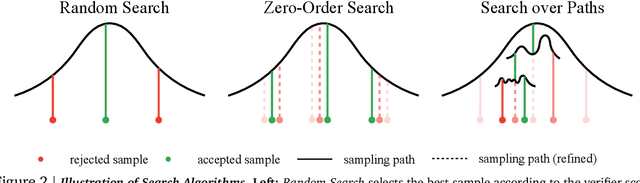
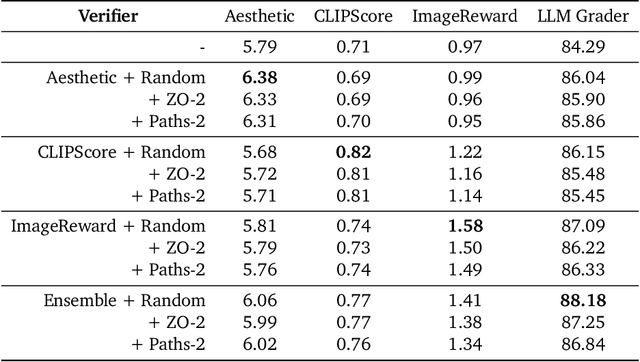
Generative models have made significant impacts across various domains, largely due to their ability to scale during training by increasing data, computational resources, and model size, a phenomenon characterized by the scaling laws. Recent research has begun to explore inference-time scaling behavior in Large Language Models (LLMs), revealing how performance can further improve with additional computation during inference. Unlike LLMs, diffusion models inherently possess the flexibility to adjust inference-time computation via the number of denoising steps, although the performance gains typically flatten after a few dozen. In this work, we explore the inference-time scaling behavior of diffusion models beyond increasing denoising steps and investigate how the generation performance can further improve with increased computation. Specifically, we consider a search problem aimed at identifying better noises for the diffusion sampling process. We structure the design space along two axes: the verifiers used to provide feedback, and the algorithms used to find better noise candidates. Through extensive experiments on class-conditioned and text-conditioned image generation benchmarks, our findings reveal that increasing inference-time compute leads to substantial improvements in the quality of samples generated by diffusion models, and with the complicated nature of images, combinations of the components in the framework can be specifically chosen to conform with different application scenario.

Stable Target Field for Reduced Variance Score Estimation in Diffusion Models

Diffusion models generate samples by reversing a fixed forward diffusion process. Despite already providing impressive empirical results, these diffusion models algorithms can be further improved by reducing the variance of the training targets in their denoising score-matching objective. We argue that the source of such variance lies in the handling of intermediate noise-variance scales, where multiple modes in the data affect the direction of reverse paths. We propose to remedy the problem by incorporating a reference batch which we use to calculate weighted conditional scores as more stable training targets. We show that the procedure indeed helps in the challenging intermediate regime by reducing (the trace of) the covariance of training targets. The new stable targets can be seen as trading bias for reduced variance, where the bias vanishes with increasing reference batch size. Empirically, we show that the new objective improves the image quality, stability, and training speed of various popular diffusion models across datasets with both general ODE and SDE solvers. When used in combination with EDM, our method yields a current SOTA FID of 1.90 with 35 network evaluations on the unconditional CIFAR-10 generation task. The code is available at https://github.com/Newbeeer/stf

PFGM++: Unlocking the Potential of Physics-Inspired Generative Models

We introduce a new family of physics-inspired generative models termed PFGM++ that unifies diffusion models and Poisson Flow Generative Models (PFGM). These models realize generative trajectories for $N$ dimensional data by embedding paths in $N{+}D$ dimensional space while still controlling the progression with a simple scalar norm of the $D$ additional variables. The new models reduce to PFGM when $D{=}1$ and to diffusion models when $D{\to}\infty$. The flexibility of choosing $D$ allows us to trade off robustness against rigidity as increasing $D$ results in more concentrated coupling between the data and the additional variable norms. We dispense with the biased large batch field targets used in PFGM and instead provide an unbiased perturbation-based objective similar to diffusion models. To explore different choices of $D$, we provide a direct alignment method for transferring well-tuned hyperparameters from diffusion models ($D{\to} \infty$) to any finite $D$ values. Our experiments show that models with finite $D$ can be superior to previous state-of-the-art diffusion models on CIFAR-10/FFHQ $64{\times}64$ datasets, with FID scores of $1.91/2.43$ when $D{=}2048/128$. In class-conditional setting, $D{=}2048$ yields current state-of-the-art FID of $1.74$ on CIFAR-10. In addition, we demonstrate that models with smaller $D$ exhibit improved robustness against modeling errors. Code is available at https://github.com/Newbeeer/pfgmpp

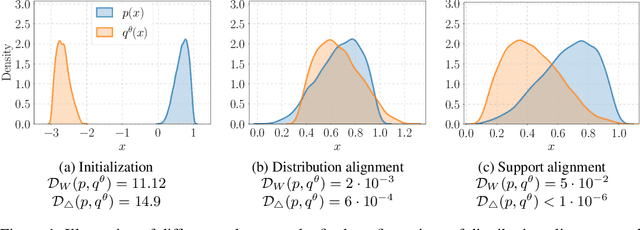
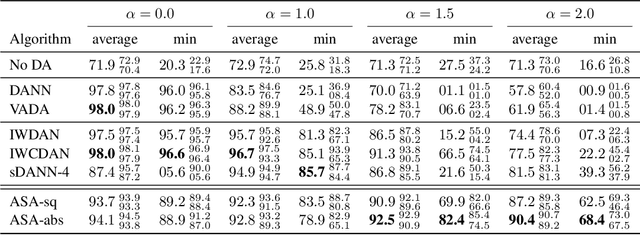
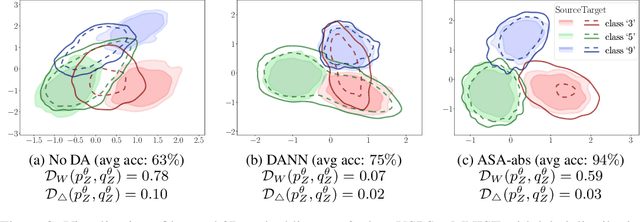
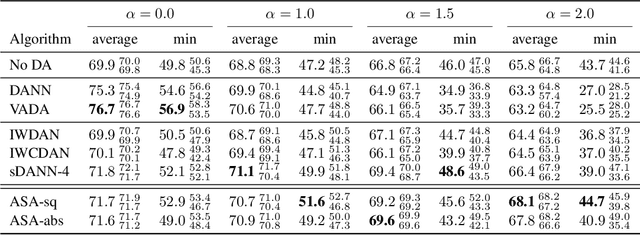
Adversarial Support Alignment

We study the problem of aligning the supports of distributions. Compared to the existing work on distribution alignment, support alignment does not require the densities to be matched. We propose symmetric support difference as a divergence measure to quantify the mismatch between supports. We show that select discriminators (e.g. discriminator trained for Jensen-Shannon divergence) are able to map support differences as support differences in their one-dimensional output space. Following this result, our method aligns supports by minimizing a symmetrized relaxed optimal transport cost in the discriminator 1D space via an adversarial process. Furthermore, we show that our approach can be viewed as a limit of existing notions of alignment by increasing transportation assignment tolerance. We quantitatively evaluate the method across domain adaptation tasks with shifts in label distributions. Our experiments show that the proposed method is more robust against these shifts than other alignment-based baselines.

The Benefits of Pairwise Discriminators for Adversarial Training

Adversarial training methods typically align distributions by solving two-player games. However, in most current formulations, even if the generator aligns perfectly with data, a sub-optimal discriminator can still drive the two apart. Absent additional regularization, the instability can manifest itself as a never-ending game. In this paper, we introduce a family of objectives by leveraging pairwise discriminators, and show that only the generator needs to converge. The alignment, if achieved, would be preserved with any discriminator. We provide sufficient conditions for local convergence; characterize the capacity balance that should guide the discriminator and generator choices; and construct examples of minimally sufficient discriminators. Empirically, we illustrate the theory and the effectiveness of our approach on synthetic examples. Moreover, we show that practical methods derived from our approach can better generate higher-resolution images.