Information Geometry of Wasserstein Statistics on Shapes and Affine Deformations

Information geometry and Wasserstein geometry are two main structures introduced in a manifold of probability distributions, and they capture its different characteristics. We study characteristics of Wasserstein geometry in the framework of Li and Zhao (2023) for the affine deformation statistical model, which is a multi-dimensional generalization of the location-scale model. We compare merits and demerits of estimators based on information geometry and Wasserstein geometry. The shape of a probability distribution and its affine deformation are separated in the Wasserstein geometry, showing its robustness against the waveform perturbation in exchange for the loss in Fisher efficiency. We show that the Wasserstein estimator is the moment estimator in the case of the elliptically symmetric affine deformation model. It coincides with the information-geometrical estimator (maximum-likelihood estimator) when and only when the waveform is Gaussian. The role of the Wasserstein efficiency is elucidated in terms of robustness against waveform change.

Deep Learning in Random Neural Fields: Numerical Experiments via Neural Tangent Kernel

A biological neural network in the cortex forms a neural field. Neurons in the field have their own receptive fields, and connection weights between two neurons are random but highly correlated when they are in close proximity in receptive fields. In this paper, we investigate such neural fields in a multilayer architecture to investigate the supervised learning of the fields. We empirically compare the performances of our field model with those of randomly connected deep networks. The behavior of a randomly connected network is investigated on the basis of the key idea of the neural tangent kernel regime, a recent development in the machine learning theory of over-parameterized networks; for most randomly connected neural networks, it is shown that global minima always exist in their small neighborhoods. We numerically show that this claim also holds for our neural fields. In more detail, our model has two structures: i) each neuron in a field has a continuously distributed receptive field, and ii) the initial connection weights are random but not independent, having correlations when the positions of neurons are close in each layer. We show that such a multilayer neural field is more robust than conventional models when input patterns are deformed by noise disturbances. Moreover, its generalization ability can be slightly superior to that of conventional models.

When Does Preconditioning Help or Hurt Generalization?

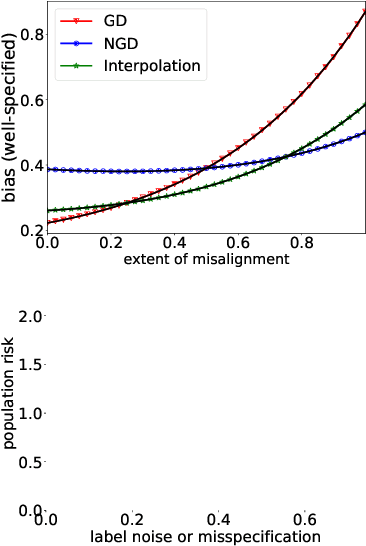
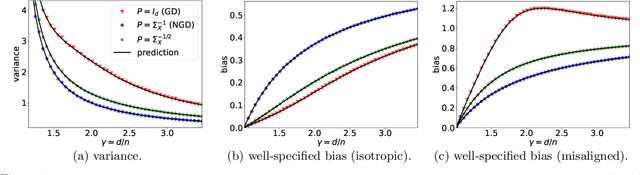
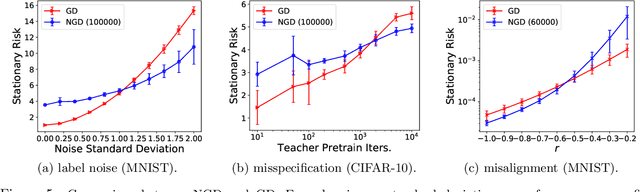
While second order optimizers such as natural gradient descent (NGD) often speed up optimization, their effect on generalization remains controversial. For instance, it has been pointed out that gradient descent (GD), in contrast to many preconditioned updates, converges to small Euclidean norm solutions in overparameterized models, leading to favorable generalization properties. This work presents a more nuanced view on the comparison of generalization between first- and second-order methods. We provide an asymptotic bias-variance decomposition of the generalization error of overparameterized ridgeless regression under a general class of preconditioner $\boldsymbol{P}$, and consider the inverse population Fisher information matrix (used in NGD) as a particular example. We determine the optimal $\boldsymbol{P}$ for both the bias and variance, and find that the relative generalization performance of different optimizers depends on the label noise and the "shape" of the signal (true parameters): when the labels are noisy, the model is misspecified, or the signal is misaligned with the features, NGD can achieve lower risk; conversely, GD generalizes better than NGD under clean labels, a well-specified model, or aligned signal. Based on this analysis, we discuss several approaches to manage the bias-variance tradeoff, and the potential benefit of interpolating between GD and NGD. We then extend our analysis to regression in the reproducing kernel Hilbert space and demonstrate that preconditioned GD can decrease the population risk faster than GD. Lastly, we empirically compare the generalization performance of first- and second-order optimizers in neural network experiments, and observe robust trends matching our theoretical analysis.

Any Target Function Exists in a Neighborhood of Any Sufficiently Wide Random Network: A Geometrical Perspective

It is known that any target function is realized in a sufficiently small neighborhood of any randomly connected deep network, provided the width (the number of neurons in a layer) is sufficiently large. There are sophisticated theories and discussions concerning this striking fact, but rigorous theories are very complicated. We give an elementary geometrical proof by using a simple model for the purpose of elucidating its structure. We show that high-dimensional geometry plays a magical role: When we project a high-dimensional sphere of radius 1 to a low-dimensional subspace, the uniform distribution over the sphere reduces to a Gaussian distribution of negligibly small covariances.

Pathological spectra of the Fisher information metric and its variants in deep neural networks

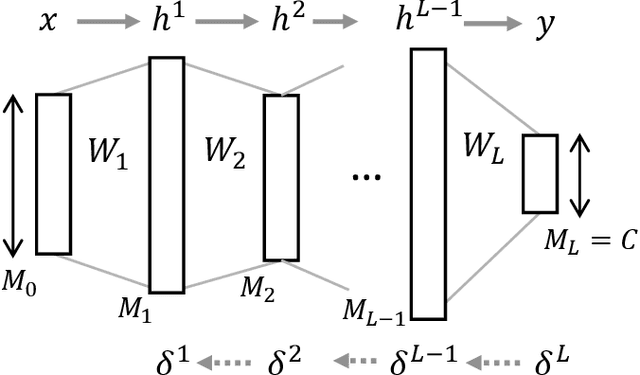
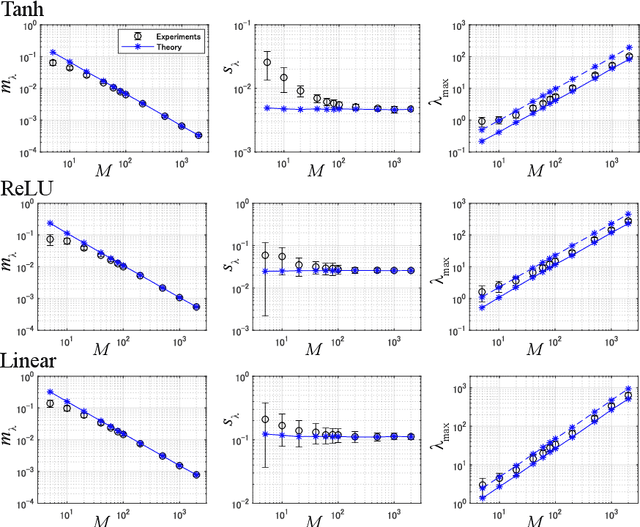
The Fisher information matrix (FIM) plays an essential role in statistics and machine learning as a Riemannian metric tensor. Focusing on the FIM and its variants in deep neural networks (DNNs), we reveal their characteristic behavior when the network is sufficiently wide and has random weights and biases. Various FIMs asymptotically show pathological eigenvalue spectra in the sense that a small number of eigenvalues take on large values while most of them are close to zero. This implies that the local shape of the parameter space or loss landscape is very steep in a few specific directions and almost flat in the other directions. Similar pathological spectra appear in other variants of FIMs: one is the neural tangent kernel; another is a metric for the input signal and feature space that arises from feedforward signal propagation. The quantitative understanding of the FIM and its variants provided here offers important perspectives on learning and signal processing in large-scale DNNs.

The Normalization Method for Alleviating Pathological Sharpness in Wide Neural Networks

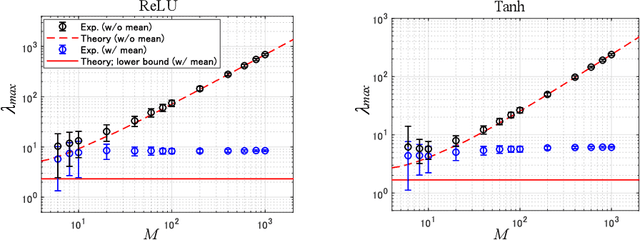
Normalization methods play an important role in enhancing the performance of deep learning while their theoretical understandings have been limited. To theoretically elucidate the effectiveness of normalization, we quantify the geometry of the parameter space determined by the Fisher information matrix (FIM), which also corresponds to the local shape of the loss landscape under certain conditions. We analyze deep neural networks with random initialization, which is known to suffer from a pathologically sharp shape of the landscape when the network becomes sufficiently wide. We reveal that batch normalization in the last layer contributes to drastically decreasing such pathological sharpness if the width and sample number satisfy a specific condition. In contrast, it is hard for batch normalization in the middle hidden layers to alleviate pathological sharpness in many settings. We also found that layer normalization cannot alleviate pathological sharpness either. Thus, we can conclude that batch normalization in the last layer significantly contributes to decreasing the sharpness induced by the FIM.

Fisher Information and Natural Gradient Learning of Random Deep Networks

A deep neural network is a hierarchical nonlinear model transforming input signals to output signals. Its input-output relation is considered to be stochastic, being described for a given input by a parameterized conditional probability distribution of outputs. The space of parameters consisting of weights and biases is a Riemannian manifold, where the metric is defined by the Fisher information matrix. The natural gradient method uses the steepest descent direction in a Riemannian manifold, so it is effective in learning, avoiding plateaus. It requires inversion of the Fisher information matrix, however, which is practically impossible when the matrix has a huge number of dimensions. Many methods for approximating the natural gradient have therefore been introduced. The present paper uses statistical neurodynamical method to reveal the properties of the Fisher information matrix in a net of random connections under the mean field approximation. We prove that the Fisher information matrix is unit-wise block diagonal supplemented by small order terms of off-block-diagonal elements, which provides a justification for the quasi-diagonal natural gradient method by Y. Ollivier. A unitwise block-diagonal Fisher metrix reduces to the tensor product of the Fisher information matrices of single units. We further prove that the Fisher information matrix of a single unit has a simple reduced form, a sum of a diagonal matrix and a rank 2 matrix of weight-bias correlations. We obtain the inverse of Fisher information explicitly. We then have an explicit form of the natural gradient, without relying on the numerical matrix inversion, which drastically speeds up stochastic gradient learning.

Statistical Neurodynamics of Deep Networks: Geometry of Signal Spaces

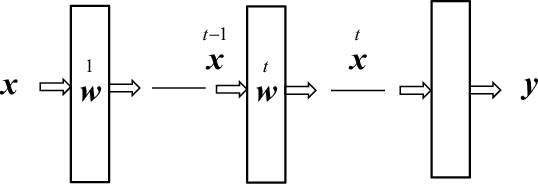
Statistical neurodynamics studies macroscopic behaviors of randomly connected neural networks. We consider a deep layered feedforward network where input signals are processed layer by layer. The manifold of input signals is embedded in a higher dimensional manifold of the next layer as a curved submanifold, provided the number of neurons is larger than that of inputs. We show geometrical features of the embedded manifold, proving that the manifold enlarges or shrinks locally isotropically so that it is always embedded conformally. We study the curvature of the embedded manifold. The scalar curvature converges to a constant or diverges to infinity slowly. The distance between two signals also changes, converging eventually to a stable fixed value, provided both the number of neurons in a layer and the number of layers tend to infinity. This causes a problem, since when we consider a curve in the input space, it is mapped as a continuous curve of fractal nature, but our theory contradictorily suggests that the curve eventually converges to a discrete set of equally spaced points. In reality, the numbers of neurons and layers are finite and thus, it is expected that the finite size effect causes the discrepancies between our theory and reality. We need to further study the discrepancies to understand their implications on information processing.

Universal Statistics of Fisher Information in Deep Neural Networks: Mean Field Approach

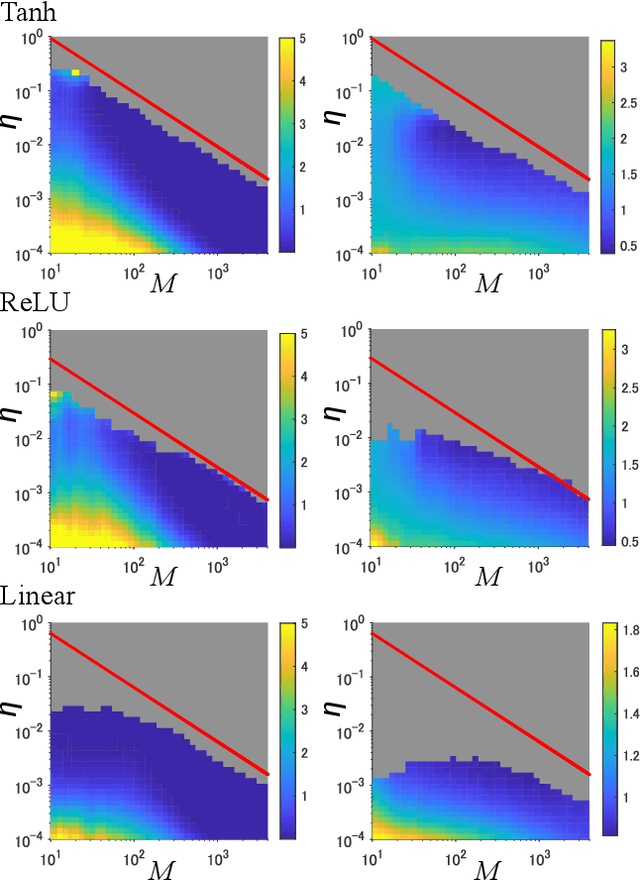
This study analyzes the Fisher information matrix (FIM) by applying mean-field theory to deep neural networks with random weights. We theoretically find novel statistics of the FIM, which are universal among a wide class of deep networks with any number of layers and various activation functions. Although most of the FIM's eigenvalues are close to zero, the maximum eigenvalue takes on a huge value and the eigenvalue distribution has an extremely long tail. These statistics suggest that the shape of a loss landscape is locally flat in most dimensions, but strongly distorted in the other dimensions. Moreover, our theory of the FIM leads to quantitative evaluation of learning in deep networks. First, the maximum eigenvalue enables us to estimate an appropriate size of a learning rate for steepest gradient methods to converge. Second, the flatness induced by the small eigenvalues is connected to generalization ability through a norm-based capacity measure.

Bayesian Robust Tensor Factorization for Incomplete Multiway Data

We propose a generative model for robust tensor factorization in the presence of both missing data and outliers. The objective is to explicitly infer the underlying low-CP-rank tensor capturing the global information and a sparse tensor capturing the local information (also considered as outliers), thus providing the robust predictive distribution over missing entries. The low-CP-rank tensor is modeled by multilinear interactions between multiple latent factors on which the column sparsity is enforced by a hierarchical prior, while the sparse tensor is modeled by a hierarchical view of Student-$t$ distribution that associates an individual hyperparameter with each element independently. For model learning, we develop an efficient closed-form variational inference under a fully Bayesian treatment, which can effectively prevent the overfitting problem and scales linearly with data size. In contrast to existing related works, our method can perform model selection automatically and implicitly without need of tuning parameters. More specifically, it can discover the groundtruth of CP rank and automatically adapt the sparsity inducing priors to various types of outliers. In addition, the tradeoff between the low-rank approximation and the sparse representation can be optimized in the sense of maximum model evidence. The extensive experiments and comparisons with many state-of-the-art algorithms on both synthetic and real-world datasets demonstrate the superiorities of our method from several perspectives.