Pathological spectra of the Fisher information metric and its variants in deep neural networks

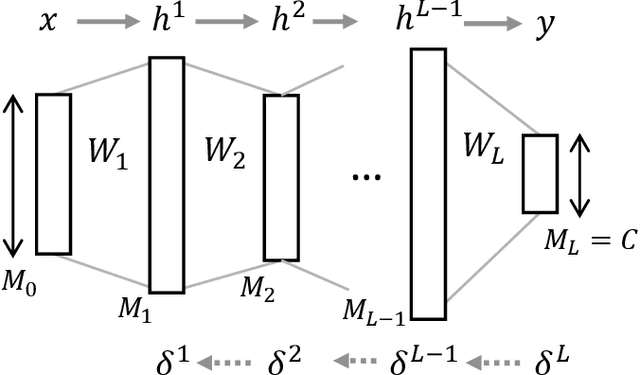
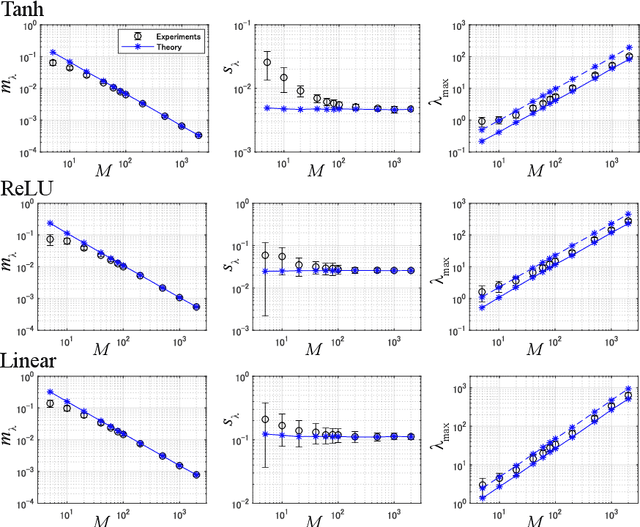
The Fisher information matrix (FIM) plays an essential role in statistics and machine learning as a Riemannian metric tensor. Focusing on the FIM and its variants in deep neural networks (DNNs), we reveal their characteristic behavior when the network is sufficiently wide and has random weights and biases. Various FIMs asymptotically show pathological eigenvalue spectra in the sense that a small number of eigenvalues take on large values while most of them are close to zero. This implies that the local shape of the parameter space or loss landscape is very steep in a few specific directions and almost flat in the other directions. Similar pathological spectra appear in other variants of FIMs: one is the neural tangent kernel; another is a metric for the input signal and feature space that arises from feedforward signal propagation. The quantitative understanding of the FIM and its variants provided here offers important perspectives on learning and signal processing in large-scale DNNs.