Geometry of EM and related iterative algorithms

The Expectation--Maximization (EM) algorithm is a simple meta-algorithm that has been used for many years as a methodology for statistical inference when there are missing measurements in the observed data or when the data is composed of observables and unobservables. Its general properties are well studied, and also, there are countless ways to apply it to individual problems. In this paper, we introduce the $em$ algorithm, an information geometric formulation of the EM algorithm, and its extensions and applications to various problems. Specifically, we will see that it is possible to formulate an outlier-robust inference algorithm, an algorithm for calculating channel capacity, parameter estimation methods on probability simplex, particular multivariate analysis methods such as principal component analysis in a space of probability models and modal regression, matrix factorization, and learning generative models, which have recently attracted attention in deep learning, from the geometric perspective.

Full-Span Log-Linear Model and Fast Learning Algorithm

The full-span log-linear(FSLL) model introduced in this paper is considered an $n$-th order Boltzmann machine, where $n$ is the number of all variables in the target system. Let $X=(X_0,...,X_{n-1})$ be finite discrete random variables that can take $|X|=|X_0|...|X_{n-1}|$ different values. The FSLL model has $|X|-1$ parameters and can represent arbitrary positive distributions of $X$. The FSLL model is a "highest-order" Boltzmann machine; nevertheless, we can compute the dual parameters of the model distribution, which plays important roles in exponential families, in $O(|X|\log|X|)$ time. Furthermore, using properties of the dual parameters of the FSLL model, we can construct an efficient learning algorithm. The FSLL model is limited to small probabilistic models up to $|X|\approx2^{25}$; however, in this problem domain, the FSLL model flexibly fits various true distributions underlying the training data without any hyperparameter tuning. The experiments presented that the FSLL successfully learned six training datasets such that $|X|=2^{20}$ within one minute with a laptop PC.

Learning Curves for Sequential Training of Neural Networks: Self-Knowledge Transfer and Forgetting

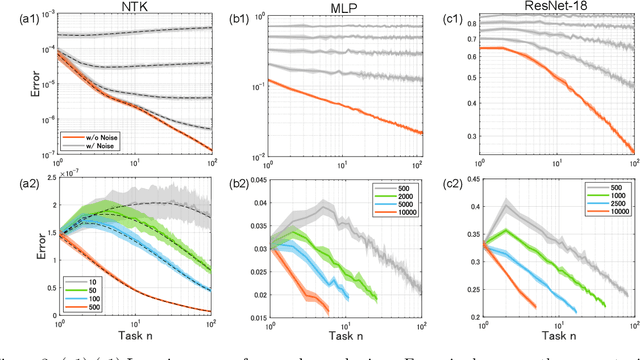
Sequential training from task to task is becoming one of the major objects in deep learning applications such as continual learning and transfer learning. Nevertheless, it remains unclear under what conditions the trained model's performance improves or deteriorates. To deepen our understanding of sequential training, this study provides a theoretical analysis of generalization performance in a solvable case of continual learning. We consider neural networks in the neural tangent kernel (NTK) regime that continually learn target functions from task to task, and investigate the generalization by using an established statistical mechanical analysis of kernel ridge-less regression. We first show characteristic transitions from positive to negative transfer. More similar targets above a specific critical value can achieve positive knowledge transfer for the subsequent task while catastrophic forgetting occurs even with very similar targets. Next, we investigate a variant of continual learning where the model learns the same target function in multiple tasks. Even for the same target, the trained model shows some transfer and forgetting depending on the sample size of each task. We can guarantee that the generalization error monotonically decreases from task to task for equal sample sizes while unbalanced sample sizes deteriorate the generalization. We respectively refer to these improvement and deterioration as self-knowledge transfer and forgetting, and empirically confirm them in realistic training of deep neural networks as well.

Principal component analysis for Gaussian process posteriors

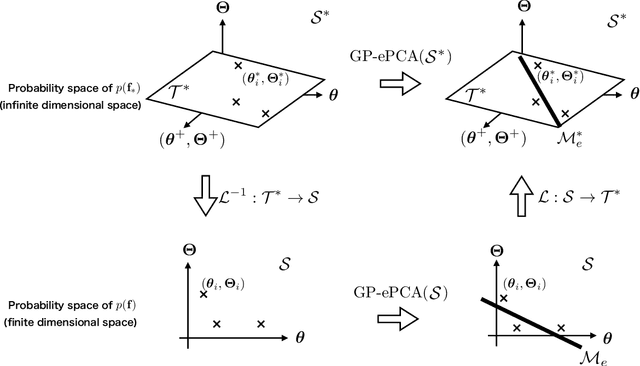
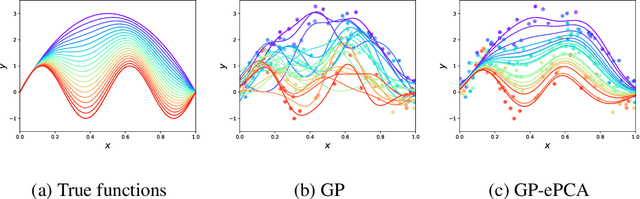
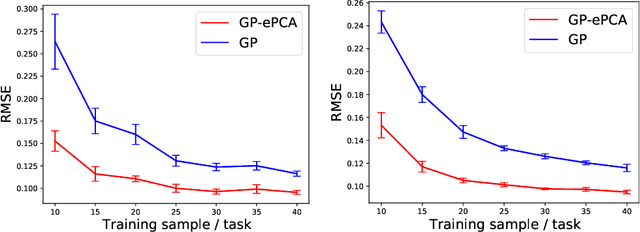
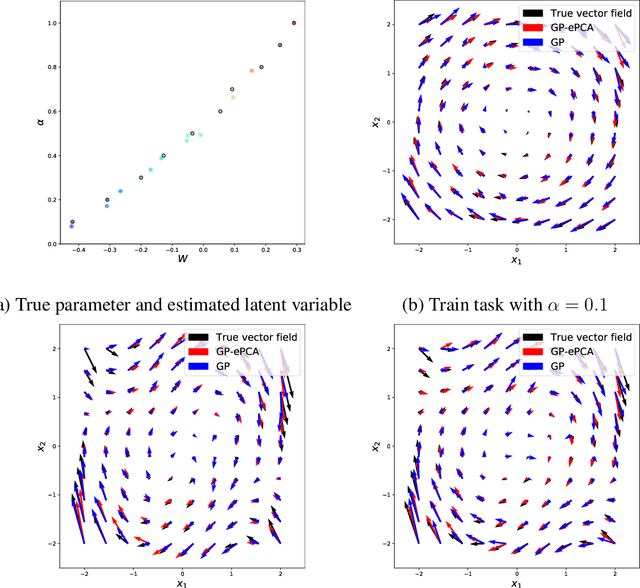
This paper proposes an extension of principal component analysis for Gaussian process posteriors denoted by GP-PCA. Since GP-PCA estimates a low-dimensional space of GP posteriors, it can be used for meta-learning, which is a framework for improving the precision of a new task by estimating a structure of a set of tasks. The issue is how to define a structure of a set of GPs with an infinite-dimensional parameter, such as coordinate system and a divergence. In this study, we reduce the infiniteness of GP to the finite-dimensional case under the information geometrical framework by considering a space of GP posteriors that has the same prior. In addition, we propose an approximation method of GP-PCA based on variational inference and demonstrate the effectiveness of GP-PCA as meta-learning through experiments.

Reconsidering Dependency Networks from an Information Geometry Perspective

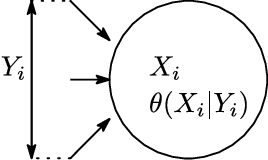
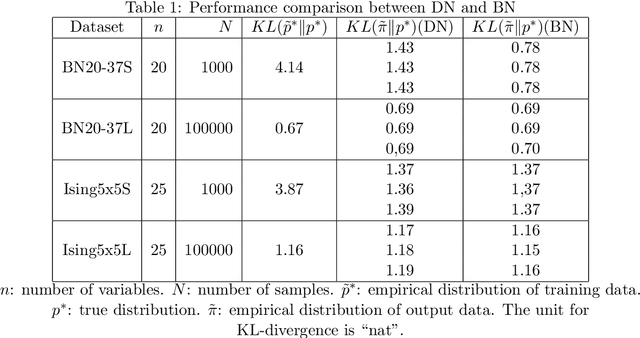
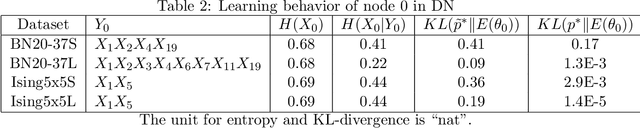
Dependency networks (Heckerman et al., 2000) are potential probabilistic graphical models for systems comprising a large number of variables. Like Bayesian networks, the structure of a dependency network is represented by a directed graph, and each node has a conditional probability table. Learning and inference are realized locally on individual nodes; therefore, computation remains tractable even with a large number of variables. However, the dependency network's learned distribution is the stationary distribution of a Markov chain called pseudo-Gibbs sampling and has no closed-form expressions. This technical disadvantage has impeded the development of dependency networks. In this paper, we consider a certain manifold for each node. Then, we can interpret pseudo-Gibbs sampling as iterative m-projections onto these manifolds. This interpretation provides a theoretical bound for the location where the stationary distribution of pseudo-Gibbs sampling exists in distribution space. Furthermore, this interpretation involves structure and parameter learning algorithms as optimization problems. In addition, we compare dependency and Bayesian networks experimentally. The results demonstrate that the dependency network and the Bayesian network have roughly the same performance in terms of the accuracy of their learned distributions. The results also show that the dependency network can learn much faster than the Bayesian network.

Pathological spectra of the Fisher information metric and its variants in deep neural networks

The Fisher information matrix (FIM) plays an essential role in statistics and machine learning as a Riemannian metric tensor. Focusing on the FIM and its variants in deep neural networks (DNNs), we reveal their characteristic behavior when the network is sufficiently wide and has random weights and biases. Various FIMs asymptotically show pathological eigenvalue spectra in the sense that a small number of eigenvalues take on large values while most of them are close to zero. This implies that the local shape of the parameter space or loss landscape is very steep in a few specific directions and almost flat in the other directions. Similar pathological spectra appear in other variants of FIMs: one is the neural tangent kernel; another is a metric for the input signal and feature space that arises from feedforward signal propagation. The quantitative understanding of the FIM and its variants provided here offers important perspectives on learning and signal processing in large-scale DNNs.

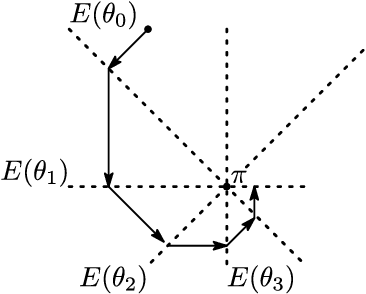
On a convergence property of a geometrical algorithm for statistical manifolds

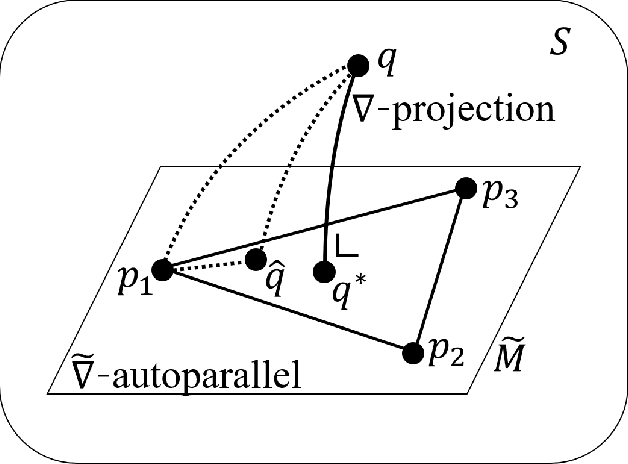
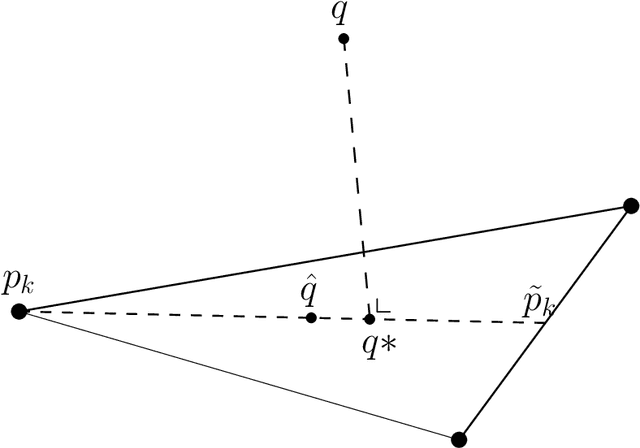
In this paper, we examine a geometrical projection algorithm for statistical inference. The algorithm is based on Pythagorean relation and it is derivative-free as well as representation-free that is useful in nonparametric cases. We derive a bound of learning rate to guarantee local convergence. In special cases of m-mixture and e-mixture estimation problems, we calculate specific forms of the bound that can be used easily in practice.

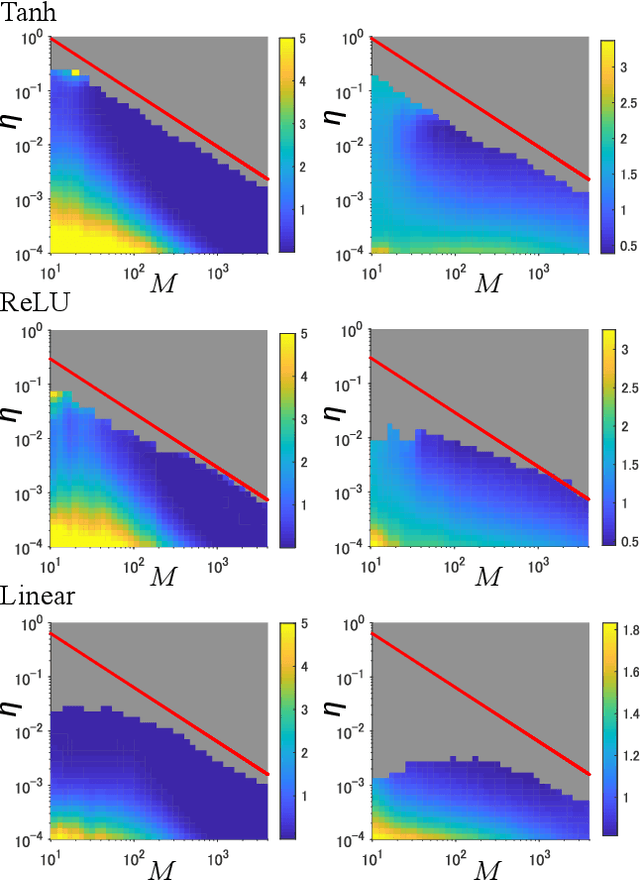
The Normalization Method for Alleviating Pathological Sharpness in Wide Neural Networks

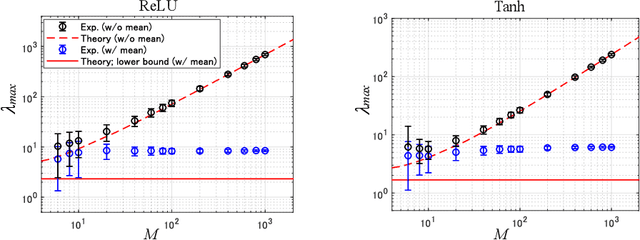
Normalization methods play an important role in enhancing the performance of deep learning while their theoretical understandings have been limited. To theoretically elucidate the effectiveness of normalization, we quantify the geometry of the parameter space determined by the Fisher information matrix (FIM), which also corresponds to the local shape of the loss landscape under certain conditions. We analyze deep neural networks with random initialization, which is known to suffer from a pathologically sharp shape of the landscape when the network becomes sufficiently wide. We reveal that batch normalization in the last layer contributes to drastically decreasing such pathological sharpness if the width and sample number satisfy a specific condition. In contrast, it is hard for batch normalization in the middle hidden layers to alleviate pathological sharpness in many settings. We also found that layer normalization cannot alleviate pathological sharpness either. Thus, we can conclude that batch normalization in the last layer significantly contributes to decreasing the sharpness induced by the FIM.

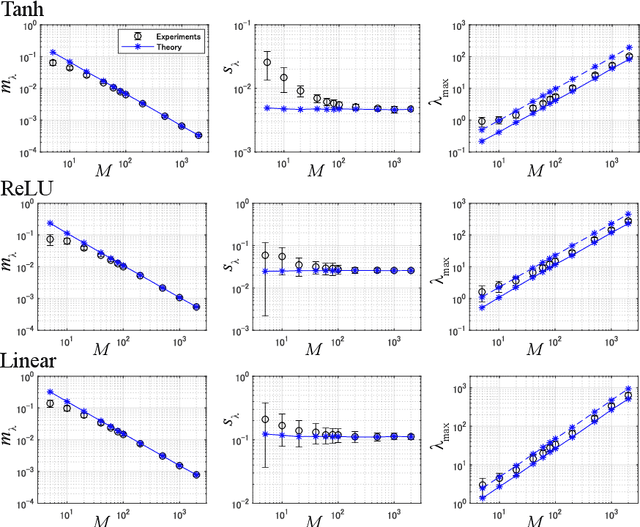
Universal Statistics of Fisher Information in Deep Neural Networks: Mean Field Approach

This study analyzes the Fisher information matrix (FIM) by applying mean-field theory to deep neural networks with random weights. We theoretically find novel statistics of the FIM, which are universal among a wide class of deep networks with any number of layers and various activation functions. Although most of the FIM's eigenvalues are close to zero, the maximum eigenvalue takes on a huge value and the eigenvalue distribution has an extremely long tail. These statistics suggest that the shape of a loss landscape is locally flat in most dimensions, but strongly distorted in the other dimensions. Moreover, our theory of the FIM leads to quantitative evaluation of learning in deep networks. First, the maximum eigenvalue enables us to estimate an appropriate size of a learning rate for steepest gradient methods to converge. Second, the flatness induced by the small eigenvalues is connected to generalization ability through a norm-based capacity measure.

Constraint-free Graphical Model with Fast Learning Algorithm

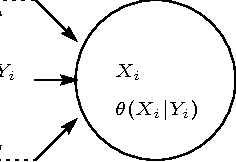
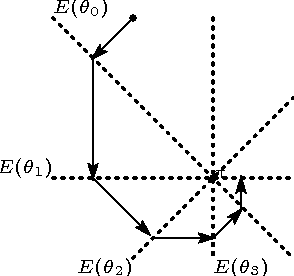
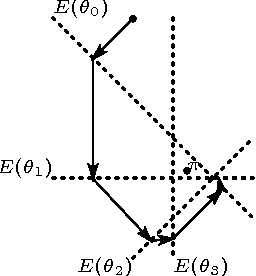
In this paper, we propose a simple, versatile model for learning the structure and parameters of multivariate distributions from a data set. Learning a Markov network from a given data set is not a simple problem, because Markov networks rigorously represent Markov properties, and this rigor imposes complex constraints on the design of the networks. Our proposed model removes these constraints, acquiring important aspects from the information geometry. The proposed parameter- and structure-learning algorithms are simple to execute as they are based solely on local computation at each node. Experiments demonstrate that our algorithms work appropriately.