Multi-task manifold learning for small sample size datasets

In this study, we develop a method for multi-task manifold learning. The method aims to improve the performance of manifold learning for multiple tasks, particularly when each task has a small number of samples. Furthermore, the method also aims to generate new samples for new tasks, in addition to new samples for existing tasks. In the proposed method, we use two different types of information transfer: instance transfer and model transfer. For instance transfer, datasets are merged among similar tasks, whereas for model transfer, the manifold models are averaged among similar tasks. For this purpose, the proposed method consists of a set of generative manifold models corresponding to the tasks, which are integrated into a general model of a fiber bundle. We applied the proposed method to artificial datasets and face image sets, and the results showed that the method was able to estimate the manifolds, even for a tiny number of samples.

Principal component analysis for Gaussian process posteriors

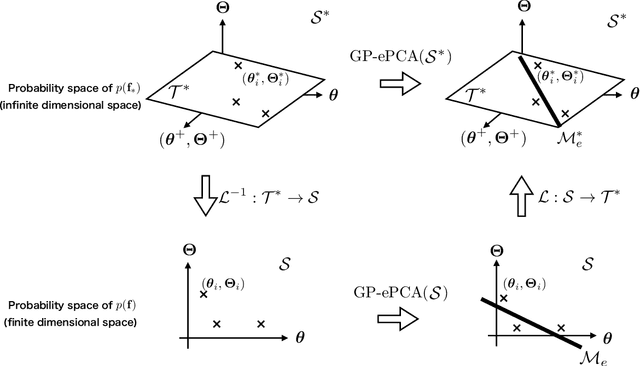
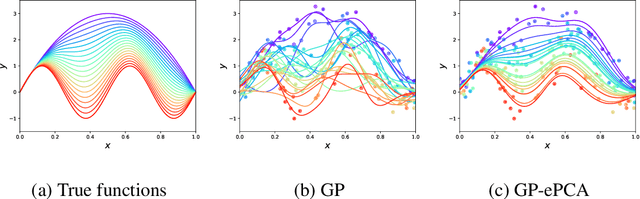
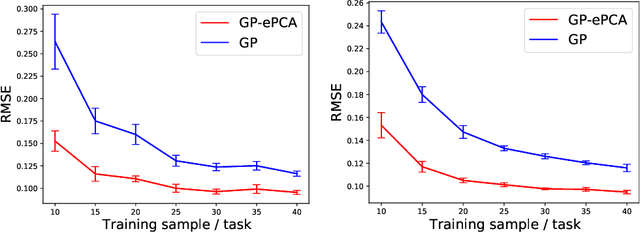
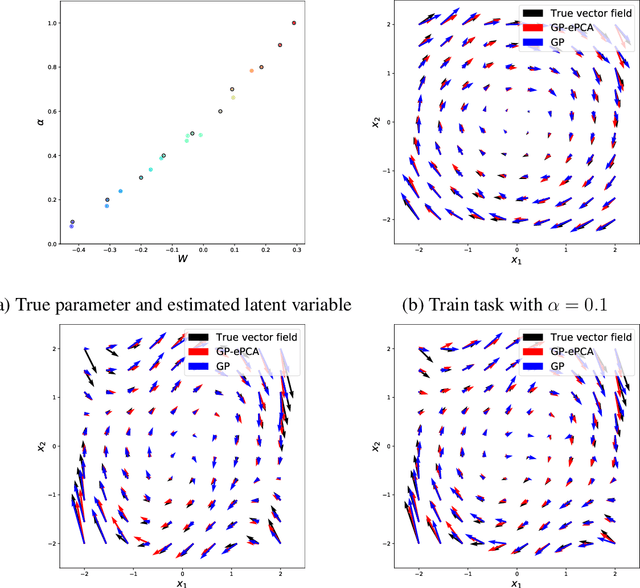
This paper proposes an extension of principal component analysis for Gaussian process posteriors denoted by GP-PCA. Since GP-PCA estimates a low-dimensional space of GP posteriors, it can be used for meta-learning, which is a framework for improving the precision of a new task by estimating a structure of a set of tasks. The issue is how to define a structure of a set of GPs with an infinite-dimensional parameter, such as coordinate system and a divergence. In this study, we reduce the infiniteness of GP to the finite-dimensional case under the information geometrical framework by considering a space of GP posteriors that has the same prior. In addition, we propose an approximation method of GP-PCA based on variational inference and demonstrate the effectiveness of GP-PCA as meta-learning through experiments.

Stopping Criterion for Active Learning Based on Error Stability

Active learning is a framework for supervised learning to improve the predictive performance by adaptively annotating a small number of samples. To realize efficient active learning, both an acquisition function that determines the next datum and a stopping criterion that determines when to stop learning should be considered. In this study, we propose a stopping criterion based on error stability, which guarantees that the change in generalization error upon adding a new sample is bounded by the annotation cost and can be applied to any Bayesian active learning. We demonstrate that the proposed criterion stops active learning at the appropriate timing for various learning models and real datasets.

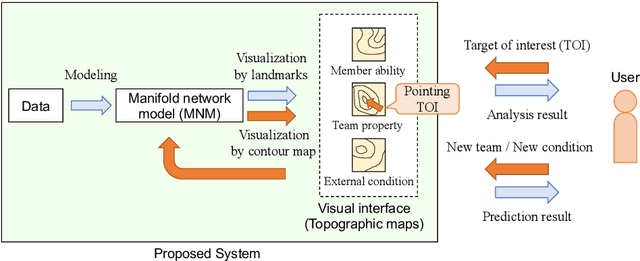
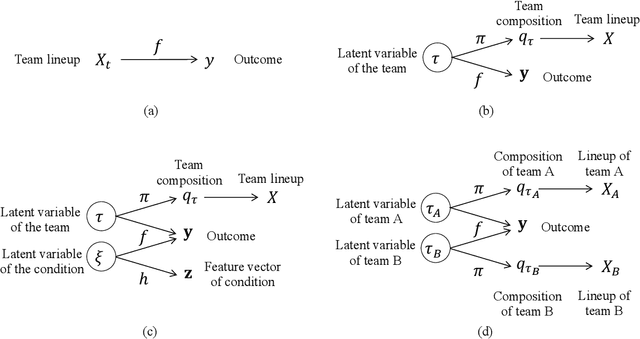
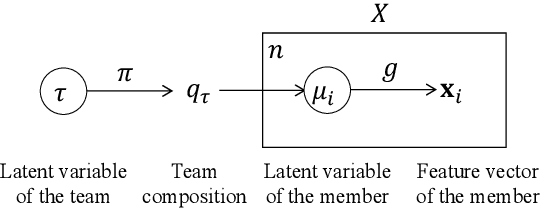
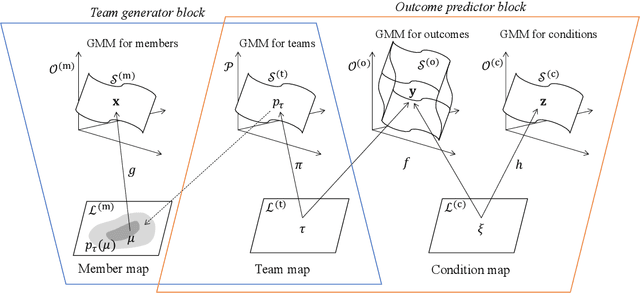
Visual analytics of set data for knowledge discovery and member selection support

Visual analytics (VA) is a visually assisted exploratory analysis approach in which knowledge discovery is executed interactively between the user and system. The purpose of this study is to develop a method for the VA of set data aimed at supporting knowledge discovery and member selection. A typical target application is a visual support system for team analysis and member selection, by which users can analyze past teams and examine candidate lineups for new teams. Because there are several difficulties, such as the combinatorial explosion problem, developing a VA system of set data is challenging. In this study, we first define the requirements that the target system should satisfy and clarify the accompanying challenges. Then we propose a method for the VA of set data, which satisfies the requirements. The key idea is to model the generation process of sets and their outputs using a manifold network model. The proposed method visualizes the relevant factors as a set of topographic maps on which various information is visualized. Furthermore, using the topographic maps as a bidirectional interface, users can indicate their targets of interest in the system on these maps. We demonstrate the proposed method by applying it to basketball teams, showing how past teams are analyzed and how new lineups are examined. Because the method can be adapted to individual application cases by extending the network structure, it can be a general method by which practical systems can be built.

Stopping criterion for active learning based on deterministic generalization bounds

Active learning is a framework in which the learning machine can select the samples to be used for training. This technique is promising, particularly when the cost of data acquisition and labeling is high. In active learning, determining the timing at which learning should be stopped is a critical issue. In this study, we propose a criterion for automatically stopping active learning. The proposed stopping criterion is based on the difference in the expected generalization errors and hypothesis testing. We derive a novel upper bound for the difference in expected generalization errors before and after obtaining a new training datum based on PAC-Bayesian theory. Unlike ordinary PAC-Bayesian bounds, though, the proposed bound is deterministic; hence, there is no uncontrollable trade-off between the confidence and tightness of the inequality. We combine the upper bound with a statistical test to derive a stopping criterion for active learning. We demonstrate the effectiveness of the proposed method via experiments with both artificial and real datasets.