Automatic Domain Adaptation by Transformers in In-Context Learning

Selecting or designing an appropriate domain adaptation algorithm for a given problem remains challenging. This paper presents a Transformer model that can provably approximate and opt for domain adaptation methods for a given dataset in the in-context learning framework, where a foundation model performs new tasks without updating its parameters at test time. Specifically, we prove that Transformers can approximate instance-based and feature-based unsupervised domain adaptation algorithms and automatically select an algorithm suited for a given dataset. Numerical results indicate that in-context learning demonstrates an adaptive domain adaptation surpassing existing methods.

Adaptive Defective Area Identification in Material Surface Using Active Transfer Learning-based Level Set Estimation

In material characterization, identifying defective areas on a material surface is fundamental. The conventional approach involves measuring the relevant physical properties point-by-point at the predetermined mesh grid points on the surface and determining the area at which the property does not reach the desired level. To identify defective areas more efficiently, we propose adaptive mapping methods in which measurement resources are used preferentially to detect the boundaries of defective areas. We interpret this problem as an active-learning (AL) of the level set estimation (LSE) problem. The goal of AL-based LSE is to determine the level set of the physical property function defined on the surface with as small number of measurements as possible. Furthermore, to handle the situations in which materials with similar specifications are repeatedly produced, we introduce a transfer learning approach so that the information of previously produced materials can be effectively utilized. As a proof-of-concept, we applied the proposed methods to the red-zone estimation problem of silicon wafers and demonstrated that we could identify the defective areas with significantly lower measurement costs than those of conventional methods.

Bayesian Active Learning for Structured Output Design

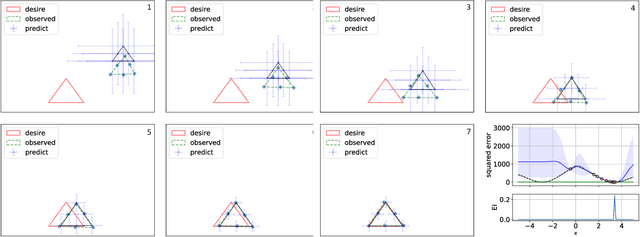
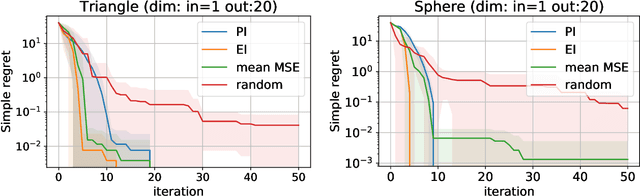
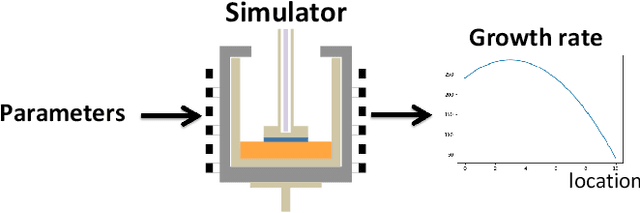
In this paper, we propose an active learning method for an inverse problem that aims to find an input that achieves a desired structured-output. The proposed method provides new acquisition functions for minimizing the error between the desired structured-output and the prediction of a Gaussian process model, by effectively incorporating the correlation between multiple outputs of the underlying multi-valued black box output functions. The effectiveness of the proposed method is verified by applying it to two synthetic shape search problem and real data. In the real data experiment, we tackle the input parameter search which achieves the desired crystal growth rate in silicon carbide (SiC) crystal growth modeling, that is a problem of materials informatics.

Variable Selection for Nonparametric Learning with Power Series Kernels

In this paper, we propose a variable selection method for general nonparametric kernel-based estimation. The proposed method consists of two-stage estimation: (1) construct a consistent estimator of the target function, (2) approximate the estimator using a few variables by l1-type penalized estimation. We see that the proposed method can be applied to various kernel nonparametric estimation such as kernel ridge regression, kernel-based density and density-ratio estimation. We prove that the proposed method has the property of the variable selection consistency when the power series kernel is used. This result is regarded as an extension of the variable selection consistency for the non-negative garrote to the kernel-based estimators. Several experiments including simulation studies and real data applications show the effectiveness of the proposed method.

Parallel Distributed Block Coordinate Descent Methods based on Pairwise Comparison Oracle

This paper provides a block coordinate descent algorithm to solve unconstrained optimization problems. In our algorithm, computation of function values or gradients is not required. Instead, pairwise comparison of function values is used. Our algorithm consists of two steps; one is the direction estimate step and the other is the search step. Both steps require only pairwise comparison of function values, which tells us only the order of function values over two points. In the direction estimate step, a Newton type search direction is estimated. A computation method like block coordinate descent methods is used with the pairwise comparison. In the search step, a numerical solution is updated along the estimated direction. The computation in the direction estimate step can be easily parallelized, and thus, the algorithm works efficiently to find the minimizer of the objective function. Also, we show an upper bound of the convergence rate. In numerical experiments, we show that our method efficiently finds the optimal solution compared to some existing methods based on the pairwise comparison.