Generalized Kernel Inducing Points by Duality Gap for Dataset Distillation

We propose Duality Gap KIP (DGKIP), an extension of the Kernel Inducing Points (KIP) method for dataset distillation. While existing dataset distillation methods often rely on bi-level optimization, DGKIP eliminates the need for such optimization by leveraging duality theory in convex programming. The KIP method has been introduced as a way to avoid bi-level optimization; however, it is limited to the squared loss and does not support other loss functions (e.g., cross-entropy or hinge loss) that are more suitable for classification tasks. DGKIP addresses this limitation by exploiting an upper bound on parameter changes after dataset distillation using the duality gap, enabling its application to a wider range of loss functions. We also characterize theoretical properties of DGKIP by providing upper bounds on the test error and prediction consistency after dataset distillation. Experimental results on standard benchmarks such as MNIST and CIFAR-10 demonstrate that DGKIP retains the efficiency of KIP while offering broader applicability and robust performance.

Distributionally Robust Coreset Selection under Covariate Shift

Coreset selection, which involves selecting a small subset from an existing training dataset, is an approach to reducing training data, and various approaches have been proposed for this method. In practical situations where these methods are employed, it is often the case that the data distributions differ between the development phase and the deployment phase, with the latter being unknown. Thus, it is challenging to select an effective subset of training data that performs well across all deployment scenarios. We therefore propose Distributionally Robust Coreset Selection (DRCS). DRCS theoretically derives an estimate of the upper bound for the worst-case test error, assuming that the future covariate distribution may deviate within a defined range from the training distribution. Furthermore, by selecting instances in a way that suppresses the estimate of the upper bound for the worst-case test error, DRCS achieves distributionally robust training instance selection. This study is primarily applicable to convex training computation, but we demonstrate that it can also be applied to deep learning under appropriate approximations. In this paper, we focus on covariate shift, a type of data distribution shift, and demonstrate the effectiveness of DRCS through experiments.

Regret Analysis for Randomized Gaussian Process Upper Confidence Bound

Gaussian process upper confidence bound (GP-UCB) is a theoretically established algorithm for Bayesian optimization (BO), where we assume the objective function $f$ follows GP. One notable drawback of GP-UCB is that the theoretical confidence parameter $\beta$ increased along with the iterations is too large. To alleviate this drawback, this paper analyzes the randomized variant of GP-UCB called improved randomized GP-UCB (IRGP-UCB), which uses the confidence parameter generated from the shifted exponential distribution. We analyze the expected regret and conditional expected regret, where the expectation and the probability are taken respectively with $f$ and noises and with the randomness of the BO algorithm. In both regret analyses, IRGP-UCB achieves a sub-linear regret upper bound without increasing the confidence parameter if the input domain is finite. Finally, we show numerical experiments using synthetic and benchmark functions and real-world emulators.

Distributionally Robust Safe Sample Screening

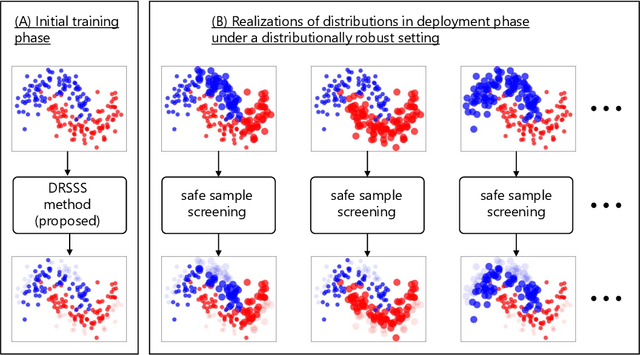
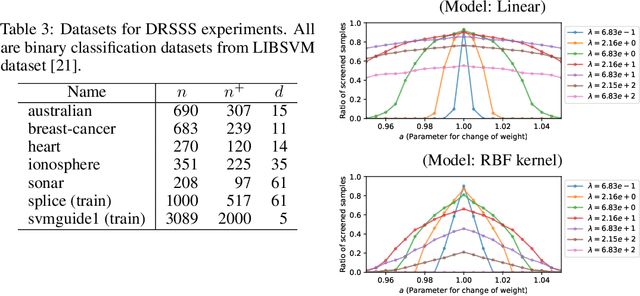
In this study, we propose a machine learning method called Distributionally Robust Safe Sample Screening (DRSSS). DRSSS aims to identify unnecessary training samples, even when the distribution of the training samples changes in the future. To achieve this, we effectively combine the distributionally robust (DR) paradigm, which aims to enhance model robustness against variations in data distribution, with the safe sample screening (SSS), which identifies unnecessary training samples prior to model training. Since we need to consider an infinite number of scenarios regarding changes in the distribution, we applied SSS because it does not require model training after the change of the distribution. In this paper, we employed the covariate shift framework to represent the distribution of training samples and reformulated the DR covariate-shift problem as a weighted empirical risk minimization problem, where the weights are subject to uncertainty within a predetermined range. By extending the existing SSS technique to accommodate this weight uncertainty, the DRSSS method is capable of reliably identifying unnecessary samples under any future distribution within a specified range. We provide a theoretical guarantee for the DRSSS method and validate its performance through numerical experiments on both synthetic and real-world datasets.

Distributionally Robust Safe Screening

In this study, we propose a method Distributionally Robust Safe Screening (DRSS), for identifying unnecessary samples and features within a DR covariate shift setting. This method effectively combines DR learning, a paradigm aimed at enhancing model robustness against variations in data distribution, with safe screening (SS), a sparse optimization technique designed to identify irrelevant samples and features prior to model training. The core concept of the DRSS method involves reformulating the DR covariate-shift problem as a weighted empirical risk minimization problem, where the weights are subject to uncertainty within a predetermined range. By extending the SS technique to accommodate this weight uncertainty, the DRSS method is capable of reliably identifying unnecessary samples and features under any future distribution within a specified range. We provide a theoretical guarantee of the DRSS method and validate its performance through numerical experiments on both synthetic and real-world datasets.

Posterior Sampling-Based Bayesian Optimization with Tighter Bayesian Regret Bounds

Among various acquisition functions (AFs) in Bayesian optimization (BO), Gaussian process upper confidence bound (GP-UCB) and Thompson sampling (TS) are well-known options with established theoretical properties regarding Bayesian cumulative regret (BCR). Recently, it has been shown that a randomized variant of GP-UCB achieves a tighter BCR bound compared with GP-UCB, which we call the tighter BCR bound for brevity. Inspired by this study, this paper first shows that TS achieves the tighter BCR bound. On the other hand, GP-UCB and TS often practically suffer from manual hyperparameter tuning and over-exploration issues, respectively. To overcome these difficulties, we propose yet another AF called a probability of improvement from the maximum of a sample path (PIMS). We show that PIMS achieves the tighter BCR bound and avoids the hyperparameter tuning, unlike GP-UCB. Furthermore, we demonstrate a wide range of experiments, focusing on the effectiveness of PIMS that mitigates the practical issues of GP-UCB and TS.

Randomized Gaussian Process Upper Confidence Bound with Tight Bayesian Regret Bounds

Gaussian process upper confidence bound (GP-UCB) is a theoretically promising approach for black-box optimization; however, the confidence parameter $\beta$ is considerably large in the theorem and chosen heuristically in practice. Then, randomized GP-UCB (RGP-UCB) uses a randomized confidence parameter, which follows the Gamma distribution, to mitigate the impact of manually specifying $\beta$. This study first generalizes the regret analysis of RGP-UCB to a wider class of distributions, including the Gamma distribution. Furthermore, we propose improved RGP-UCB (IRGP-UCB) based on a two-parameter exponential distribution, which achieves tight Bayesian regret bounds. IRGP-UCB does not require an increase in the confidence parameter in terms of the number of iterations, which avoids over-exploration in the later iterations. Finally, we demonstrate the effectiveness of IRGP-UCB through extensive experiments.

Distributionally Robust Multi-objective Bayesian Optimization under Uncertain Environments

In this study, we address the problem of optimizing multi-output black-box functions under uncertain environments. We formulate this problem as the estimation of the uncertain Pareto-frontier (PF) of a multi-output Bayesian surrogate model with two types of variables: design variables and environmental variables. We consider this problem within the context of Bayesian optimization (BO) under uncertain environments, where the design variables are controllable, whereas the environmental variables are assumed to be random and not controllable. The challenge of this problem is to robustly estimate the PF when the distribution of the environmental variables is unknown, that is, to estimate the PF when the environmental variables are generated from the worst possible distribution. We propose a method for solving the BO problem by appropriately incorporating the uncertainties of the environmental variables and their probability distribution. We demonstrate that the proposed method can find an arbitrarily accurate PF with high probability in a finite number of iterations. We also evaluate the performance of the proposed method through numerical experiments.

Bayesian Optimization for Distributionally Robust Chance-constrained Problem

In black-box function optimization, we need to consider not only controllable design variables but also uncontrollable stochastic environment variables. In such cases, it is necessary to solve the optimization problem by taking into account the uncertainty of the environmental variables. Chance-constrained (CC) problem, the problem of maximizing the expected value under a certain level of constraint satisfaction probability, is one of the practically important problems in the presence of environmental variables. In this study, we consider distributionally robust CC (DRCC) problem and propose a novel DRCC Bayesian optimization method for the case where the distribution of the environmental variables cannot be precisely specified. We show that the proposed method can find an arbitrary accurate solution with high probability in a finite number of trials, and confirm the usefulness of the proposed method through numerical experiments.

Bayesian Optimization for Cascade-type Multi-stage Processes

Complex processes in science and engineering are often formulated as multi-stage decision-making problems. In this paper, we consider a type of multi-stage decision-making process called a cascade process. A cascade process is a multi-stage process in which the output of one stage is used as an input for the next stage. When the cost of each stage is expensive, it is difficult to search for the optimal controllable parameters for each stage exhaustively. To address this problem, we formulate the optimization of the cascade process as an extension of Bayesian optimization framework and propose two types of acquisition functions (AFs) based on credible intervals and expected improvement. We investigate the theoretical properties of the proposed AFs and demonstrate their effectiveness through numerical experiments. In addition, we consider an extension called suspension setting in which we are allowed to suspend the cascade process at the middle of the multi-stage decision-making process that often arises in practical problems. We apply the proposed method in the optimization problem of the solar cell simulator, which was the motivation for this study.