Near-Optimal Algorithm for Non-Stationary Kernelized Bandits

This paper studies a non-stationary kernelized bandit (KB) problem, also called time-varying Bayesian optimization, where one seeks to minimize the regret under an unknown reward function that varies over time. In particular, we focus on a near-optimal algorithm whose regret upper bound matches the regret lower bound. For this goal, we show the first algorithm-independent regret lower bound for non-stationary KB with squared exponential and Mat\'ern kernels, which reveals that an existing optimization-based KB algorithm with slight modification is near-optimal. However, this existing algorithm suffers from feasibility issues due to its huge computational cost. Therefore, we propose a novel near-optimal algorithm called restarting phased elimination with random permutation (R-PERP), which bypasses the huge computational cost. A technical key point is the simple permutation procedures of query candidates, which enable us to derive a novel tighter confidence bound tailored to the non-stationary problems.

Bayesian Optimization for Cascade-type Multi-stage Processes

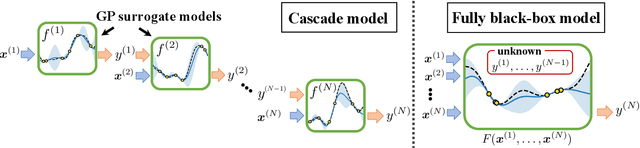
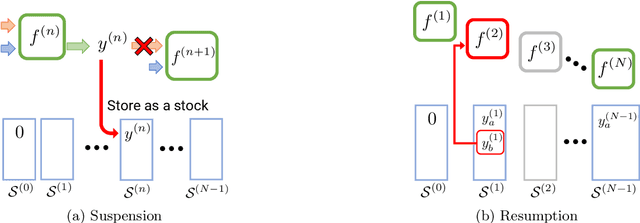
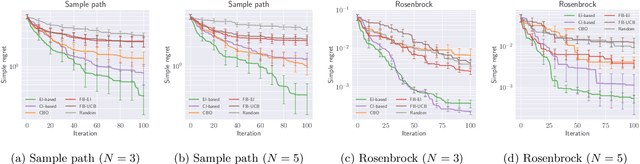
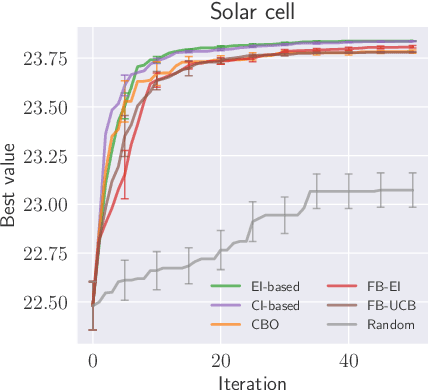
Complex processes in science and engineering are often formulated as multi-stage decision-making problems. In this paper, we consider a type of multi-stage decision-making process called a cascade process. A cascade process is a multi-stage process in which the output of one stage is used as an input for the next stage. When the cost of each stage is expensive, it is difficult to search for the optimal controllable parameters for each stage exhaustively. To address this problem, we formulate the optimization of the cascade process as an extension of Bayesian optimization framework and propose two types of acquisition functions (AFs) based on credible intervals and expected improvement. We investigate the theoretical properties of the proposed AFs and demonstrate their effectiveness through numerical experiments. In addition, we consider an extension called suspension setting in which we are allowed to suspend the cascade process at the middle of the multi-stage decision-making process that often arises in practical problems. We apply the proposed method in the optimization problem of the solar cell simulator, which was the motivation for this study.

Active learning for distributionally robust level-set estimation

Many cases exist in which a black-box function $f$ with high evaluation cost depends on two types of variables $\bm x$ and $\bm w$, where $\bm x$ is a controllable \emph{design} variable and $\bm w$ are uncontrollable \emph{environmental} variables that have random variation following a certain distribution $P$. In such cases, an important task is to find the range of design variables $\bm x$ such that the function $f(\bm x, \bm w)$ has the desired properties by incorporating the random variation of the environmental variables $\bm w$. A natural measure of robustness is the probability that $f(\bm x, \bm w)$ exceeds a given threshold $h$, which is known as the \emph{probability threshold robustness} (PTR) measure in the literature on robust optimization. However, this robustness measure cannot be correctly evaluated when the distribution $P$ is unknown. In this study, we addressed this problem by considering the \textit{distributionally robust PTR} (DRPTR) measure, which considers the worst-case PTR within given candidate distributions. Specifically, we studied the problem of efficiently identifying a reliable set $H$, which is defined as a region in which the DRPTR measure exceeds a certain desired probability $\alpha$, which can be interpreted as a level set estimation (LSE) problem for DRPTR. We propose a theoretically grounded and computationally efficient active learning method for this problem. We show that the proposed method has theoretical guarantees on convergence and accuracy, and confirmed through numerical experiments that the proposed method outperforms existing methods.

Quantifying Statistical Significance of Neural Network Representation-Driven Hypotheses by Selective Inference

In the past few years, various approaches have been developed to explain and interpret deep neural network (DNN) representations, but it has been pointed out that these representations are sometimes unstable and not reproducible. In this paper, we interpret these representations as hypotheses driven by DNN (called DNN-driven hypotheses) and propose a method to quantify the reliability of these hypotheses in statistical hypothesis testing framework. To this end, we introduce Selective Inference (SI) framework, which has received much attention in the past few years as a new statistical inference framework for data-driven hypotheses. The basic idea of SI is to make conditional inferences on the selected hypotheses under the condition that they are selected. In order to use SI framework for DNN representations, we develop a new SI algorithm based on homotopy method which enables us to derive the exact (non-asymptotic) conditional sampling distribution of the DNN-driven hypotheses. We conduct experiments on both synthetic and real-world datasets, through which we offer evidence that our proposed method can successfully control the false positive rate, has decent performance in terms of computational efficiency, and provides good results in practical applications.

Mean-Variance Analysis in Bayesian Optimization under Uncertainty

We consider active learning (AL) in an uncertain environment in which trade-off between multiple risk measures need to be considered. As an AL problem in such an uncertain environment, we study Mean-Variance Analysis in Bayesian Optimization (MVA-BO) setting. Mean-variance analysis was developed in the field of financial engineering and has been used to make decisions that take into account the trade-off between the average and variance of investment uncertainty. In this paper, we specifically focus on BO setting with an uncertain component and consider multi-task, multi-objective, and constrained optimization scenarios for the mean-variance trade-off of the uncertain component. When the target blackbox function is modeled by Gaussian Process (GP), we derive the bounds of the two risk measures and propose AL algorithm for each of the above three problems based on the risk measure bounds. We show the effectiveness of the proposed AL algorithms through theoretical analysis and numerical experiments.

Bayesian Quadrature Optimization for Probability Threshold Robustness Measure

In many product development problems, the performance of the product is governed by two types of parameters called design parameter and environmental parameter. While the former is fully controllable, the latter varies depending on the environment in which the product is used. The challenge of such a problem is to find the design parameter that maximizes the probability that the performance of the product will meet the desired requisite level given the variation of the environmental parameter. In this paper, we formulate this practical problem as active learning (AL) problems and propose efficient algorithms with theoretically guaranteed performance. Our basic idea is to use Gaussian Process (GP) model as the surrogate model of the product development process, and then to formulate our AL problems as Bayesian Quadrature Optimization problems for probabilistic threshold robustness (PTR) measure. We derive credible intervals for the PTR measure and propose AL algorithms for the optimization and level set estimation of the PTR measure. We clarify the theoretical properties of the proposed algorithms and demonstrate their efficiency in both synthetic and real-world product development problems.

Bayesian Experimental Design for Finding Reliable Level Set under Input Uncertainty

In the manufacturing industry, it is often necessary to repeat expensive operational testing of machine in order to identify the range of input conditions under which the machine operates properly. Since it is often difficult to accurately control the input conditions during the actual usage of the machine, there is a need to guarantee the performance of the machine after properly incorporating the possible variation in input conditions. In this paper, we formulate this practical manufacturing scenario as an Input Uncertain Reliable Level Set Estimation (IU-rLSE) problem, and provide an efficient algorithm for solving it. The goal of IU-rLSE is to identify the input range in which the outputs smaller/greater than a desired threshold can be obtained with high probability when the input uncertainty is properly taken into consideration. We propose an active learning method to solve the IU-rLSE problem efficiently, theoretically analyze its accuracy and convergence, and illustrate its empirical performance through numerical experiments on artificial and real data.