Adaptive Defective Area Identification in Material Surface Using Active Transfer Learning-based Level Set Estimation

In material characterization, identifying defective areas on a material surface is fundamental. The conventional approach involves measuring the relevant physical properties point-by-point at the predetermined mesh grid points on the surface and determining the area at which the property does not reach the desired level. To identify defective areas more efficiently, we propose adaptive mapping methods in which measurement resources are used preferentially to detect the boundaries of defective areas. We interpret this problem as an active-learning (AL) of the level set estimation (LSE) problem. The goal of AL-based LSE is to determine the level set of the physical property function defined on the surface with as small number of measurements as possible. Furthermore, to handle the situations in which materials with similar specifications are repeatedly produced, we introduce a transfer learning approach so that the information of previously produced materials can be effectively utilized. As a proof-of-concept, we applied the proposed methods to the red-zone estimation problem of silicon wafers and demonstrated that we could identify the defective areas with significantly lower measurement costs than those of conventional methods.

Bayesian Optimization for Cascade-type Multi-stage Processes

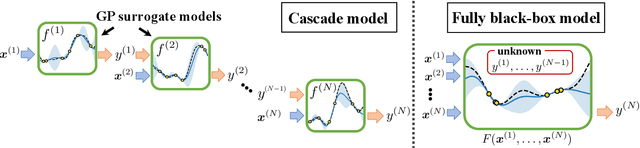
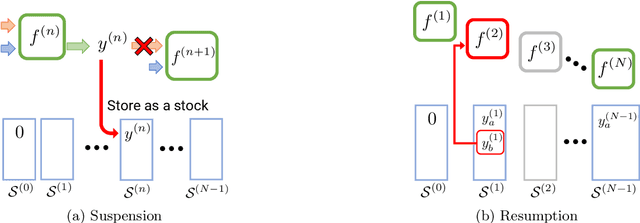
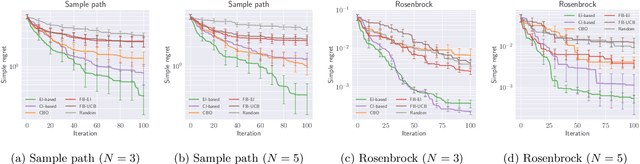
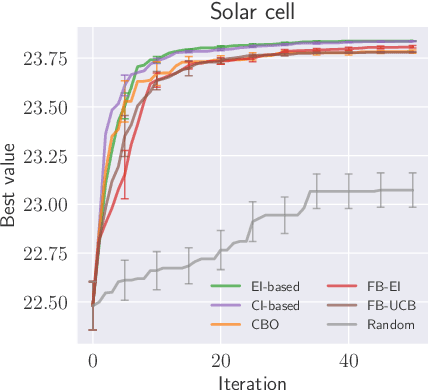
Complex processes in science and engineering are often formulated as multi-stage decision-making problems. In this paper, we consider a type of multi-stage decision-making process called a cascade process. A cascade process is a multi-stage process in which the output of one stage is used as an input for the next stage. When the cost of each stage is expensive, it is difficult to search for the optimal controllable parameters for each stage exhaustively. To address this problem, we formulate the optimization of the cascade process as an extension of Bayesian optimization framework and propose two types of acquisition functions (AFs) based on credible intervals and expected improvement. We investigate the theoretical properties of the proposed AFs and demonstrate their effectiveness through numerical experiments. In addition, we consider an extension called suspension setting in which we are allowed to suspend the cascade process at the middle of the multi-stage decision-making process that often arises in practical problems. We apply the proposed method in the optimization problem of the solar cell simulator, which was the motivation for this study.

Bayesian Active Learning for Structured Output Design

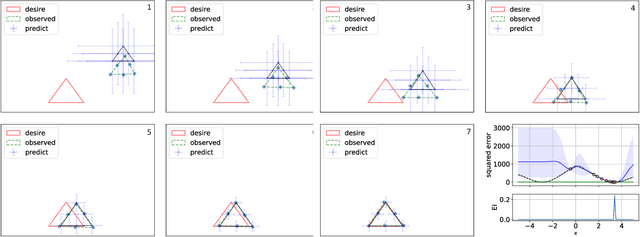
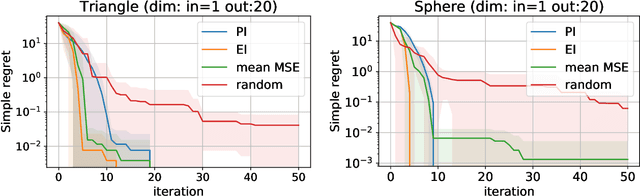
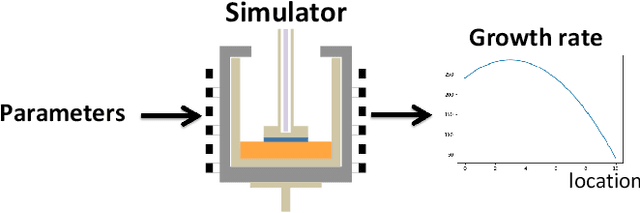
In this paper, we propose an active learning method for an inverse problem that aims to find an input that achieves a desired structured-output. The proposed method provides new acquisition functions for minimizing the error between the desired structured-output and the prediction of a Gaussian process model, by effectively incorporating the correlation between multiple outputs of the underlying multi-valued black box output functions. The effectiveness of the proposed method is verified by applying it to two synthetic shape search problem and real data. In the real data experiment, we tackle the input parameter search which achieves the desired crystal growth rate in silicon carbide (SiC) crystal growth modeling, that is a problem of materials informatics.