Bayesian Optimization for Simultaneous Selection of Machine Learning Algorithms and Hyperparameters on Shared Latent Space

Selecting the optimal combination of a machine learning (ML) algorithm and its hyper-parameters is crucial for the development of high-performance ML systems. However, since the combination of ML algorithms and hyper-parameters is enormous, the exhaustive validation requires a significant amount of time. Many existing studies use Bayesian optimization (BO) for accelerating the search. On the other hand, a significant difficulty is that, in general, there exists a different hyper-parameter space for each one of candidate ML algorithms. BO-based approaches typically build a surrogate model independently for each hyper-parameter space, by which sufficient observations are required for all candidate ML algorithms. In this study, our proposed method embeds different hyper-parameter spaces into a shared latent space, in which a surrogate multi-task model for BO is estimated. This approach can share information of observations from different ML algorithms by which efficient optimization is expected with a smaller number of total observations. We further propose the pre-training of the latent space embedding with an adversarial regularization, and a ranking model for selecting an effective pre-trained embedding for a given target dataset. Our empirical study demonstrates effectiveness of the proposed method through datasets from OpenML.

Pareto-frontier Entropy Search with Variational Lower Bound Maximization

This study considers multi-objective Bayesian optimization (MOBO) through the information gain of the Pareto-frontier. To calculate the information gain, a predictive distribution conditioned on the Pareto-frontier plays a key role, which is defined as a distribution truncated by the Pareto-frontier. However, it is usually impossible to obtain the entire Pareto-frontier in a continuous domain, and therefore, the complete truncation cannot be known. We consider an approximation of the truncate distribution by using a mixture distribution consisting of two possible approximate truncation obtainable from a subset of the Pareto-frontier, which we call over- and under-truncation. Since the optimal balance of the mixture is unknown beforehand, we propose optimizing the balancing coefficient through the variational lower bound maximization framework, by which the approximation error of the information gain can be minimized. Our empirical evaluation demonstrates the effectiveness of the proposed method particularly when the number of objective functions is large.

Regret Analysis for Randomized Gaussian Process Upper Confidence Bound

Gaussian process upper confidence bound (GP-UCB) is a theoretically established algorithm for Bayesian optimization (BO), where we assume the objective function $f$ follows GP. One notable drawback of GP-UCB is that the theoretical confidence parameter $\beta$ increased along with the iterations is too large. To alleviate this drawback, this paper analyzes the randomized variant of GP-UCB called improved randomized GP-UCB (IRGP-UCB), which uses the confidence parameter generated from the shifted exponential distribution. We analyze the expected regret and conditional expected regret, where the expectation and the probability are taken respectively with $f$ and noises and with the randomness of the BO algorithm. In both regret analyses, IRGP-UCB achieves a sub-linear regret upper bound without increasing the confidence parameter if the input domain is finite. Finally, we show numerical experiments using synthetic and benchmark functions and real-world emulators.

Learning Attributed Graphlets: Predictive Graph Mining by Graphlets with Trainable Attribute

The graph classification problem has been widely studied; however, achieving an interpretable model with high predictive performance remains a challenging issue. This paper proposes an interpretable classification algorithm for attributed graph data, called LAGRA (Learning Attributed GRAphlets). LAGRA learns importance weights for small attributed subgraphs, called attributed graphlets (AGs), while simultaneously optimizing their attribute vectors. This enables us to obtain a combination of subgraph structures and their attribute vectors that strongly contribute to discriminating different classes. A significant characteristics of LAGRA is that all the subgraph structures in the training dataset can be considered as a candidate structures of AGs. This approach can explore all the potentially important subgraphs exhaustively, but obviously, a naive implementation can require a large amount of computations. To mitigate this issue, we propose an efficient pruning strategy by combining the proximal gradient descent and a graph mining tree search. Our pruning strategy can ensure that the quality of the solution is maintained compared to the result without pruning. We empirically demonstrate that LAGRA has superior or comparable prediction performance to the standard existing algorithms including graph neural networks, while using only a small number of AGs in an interpretable manner.

Multi-Objective Bayesian Optimization with Active Preference Learning

There are a lot of real-world black-box optimization problems that need to optimize multiple criteria simultaneously. However, in a multi-objective optimization (MOO) problem, identifying the whole Pareto front requires the prohibitive search cost, while in many practical scenarios, the decision maker (DM) only needs a specific solution among the set of the Pareto optimal solutions. We propose a Bayesian optimization (BO) approach to identifying the most preferred solution in the MOO with expensive objective functions, in which a Bayesian preference model of the DM is adaptively estimated by an interactive manner based on the two types of supervisions called the pairwise preference and improvement request. To explore the most preferred solution, we define an acquisition function in which the uncertainty both in the objective functions and the DM preference is incorporated. Further, to minimize the interaction cost with the DM, we also propose an active learning strategy for the preference estimation. We empirically demonstrate the effectiveness of our proposed method through the benchmark function optimization and the hyper-parameter optimization problems for machine learning models.

Posterior Sampling-Based Bayesian Optimization with Tighter Bayesian Regret Bounds

Among various acquisition functions (AFs) in Bayesian optimization (BO), Gaussian process upper confidence bound (GP-UCB) and Thompson sampling (TS) are well-known options with established theoretical properties regarding Bayesian cumulative regret (BCR). Recently, it has been shown that a randomized variant of GP-UCB achieves a tighter BCR bound compared with GP-UCB, which we call the tighter BCR bound for brevity. Inspired by this study, this paper first shows that TS achieves the tighter BCR bound. On the other hand, GP-UCB and TS often practically suffer from manual hyperparameter tuning and over-exploration issues, respectively. To overcome these difficulties, we propose yet another AF called a probability of improvement from the maximum of a sample path (PIMS). We show that PIMS achieves the tighter BCR bound and avoids the hyperparameter tuning, unlike GP-UCB. Furthermore, we demonstrate a wide range of experiments, focusing on the effectiveness of PIMS that mitigates the practical issues of GP-UCB and TS.

Towards Practical Preferential Bayesian Optimization with Skew Gaussian Processes

We study preferential Bayesian optimization (BO) where reliable feedback is limited to pairwise comparison called duels. An important challenge in preferential BO, which uses the preferential Gaussian process (GP) model to represent flexible preference structure, is that the posterior distribution is a computationally intractable skew GP. The most widely used approach for preferential BO is Gaussian approximation, which ignores the skewness of the true posterior. Alternatively, Markov chain Monte Carlo (MCMC) based preferential BO is also proposed. In this work, we first verify the accuracy of Gaussian approximation, from which we reveal the critical problem that the predictive probability of duels can be inaccurate. This observation motivates us to improve the MCMC-based estimation for skew GP, for which we show the practical efficiency of Gibbs sampling and derive the low variance MC estimator. However, the computational time of MCMC can still be a bottleneck in practice. Towards building a more practical preferential BO, we develop a new method that achieves both high computational efficiency and low sample complexity, and then demonstrate its effectiveness through extensive numerical experiments.

Randomized Gaussian Process Upper Confidence Bound with Tight Bayesian Regret Bounds

Gaussian process upper confidence bound (GP-UCB) is a theoretically promising approach for black-box optimization; however, the confidence parameter $\beta$ is considerably large in the theorem and chosen heuristically in practice. Then, randomized GP-UCB (RGP-UCB) uses a randomized confidence parameter, which follows the Gamma distribution, to mitigate the impact of manually specifying $\beta$. This study first generalizes the regret analysis of RGP-UCB to a wider class of distributions, including the Gamma distribution. Furthermore, we propose improved RGP-UCB (IRGP-UCB) based on a two-parameter exponential distribution, which achieves tight Bayesian regret bounds. IRGP-UCB does not require an increase in the confidence parameter in terms of the number of iterations, which avoids over-exploration in the later iterations. Finally, we demonstrate the effectiveness of IRGP-UCB through extensive experiments.

Bayesian Optimization for Distributionally Robust Chance-constrained Problem

In black-box function optimization, we need to consider not only controllable design variables but also uncontrollable stochastic environment variables. In such cases, it is necessary to solve the optimization problem by taking into account the uncertainty of the environmental variables. Chance-constrained (CC) problem, the problem of maximizing the expected value under a certain level of constraint satisfaction probability, is one of the practically important problems in the presence of environmental variables. In this study, we consider distributionally robust CC (DRCC) problem and propose a novel DRCC Bayesian optimization method for the case where the distribution of the environmental variables cannot be precisely specified. We show that the proposed method can find an arbitrary accurate solution with high probability in a finite number of trials, and confirm the usefulness of the proposed method through numerical experiments.

Bayesian Optimization for Cascade-type Multi-stage Processes

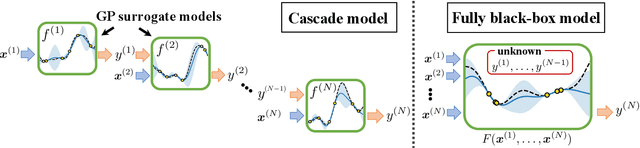
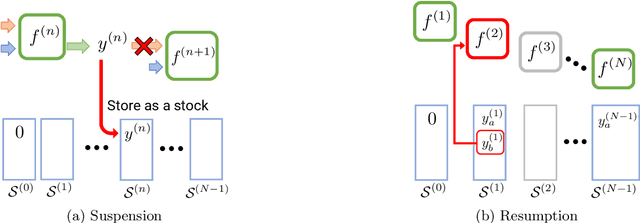
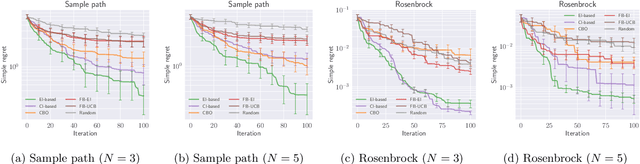
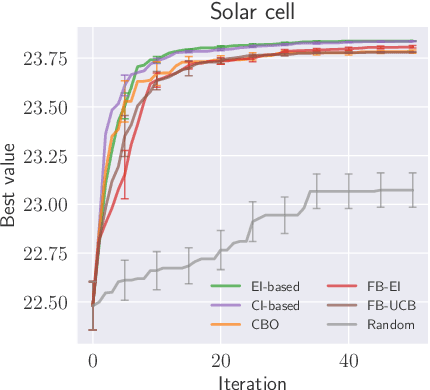
Complex processes in science and engineering are often formulated as multi-stage decision-making problems. In this paper, we consider a type of multi-stage decision-making process called a cascade process. A cascade process is a multi-stage process in which the output of one stage is used as an input for the next stage. When the cost of each stage is expensive, it is difficult to search for the optimal controllable parameters for each stage exhaustively. To address this problem, we formulate the optimization of the cascade process as an extension of Bayesian optimization framework and propose two types of acquisition functions (AFs) based on credible intervals and expected improvement. We investigate the theoretical properties of the proposed AFs and demonstrate their effectiveness through numerical experiments. In addition, we consider an extension called suspension setting in which we are allowed to suspend the cascade process at the middle of the multi-stage decision-making process that often arises in practical problems. We apply the proposed method in the optimization problem of the solar cell simulator, which was the motivation for this study.