Bayesian Active Learning for Structured Output Design
Paper and Code
Nov 09, 2019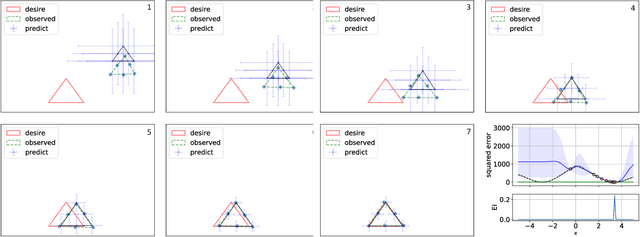

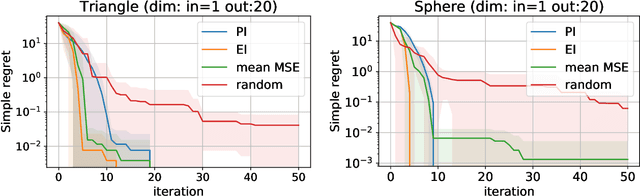
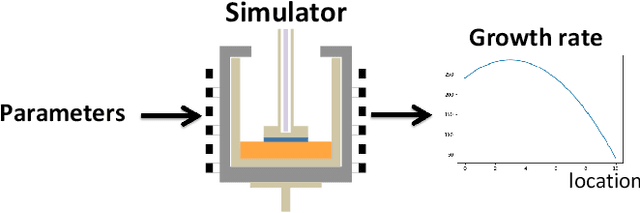
In this paper, we propose an active learning method for an inverse problem that aims to find an input that achieves a desired structured-output. The proposed method provides new acquisition functions for minimizing the error between the desired structured-output and the prediction of a Gaussian process model, by effectively incorporating the correlation between multiple outputs of the underlying multi-valued black box output functions. The effectiveness of the proposed method is verified by applying it to two synthetic shape search problem and real data. In the real data experiment, we tackle the input parameter search which achieves the desired crystal growth rate in silicon carbide (SiC) crystal growth modeling, that is a problem of materials informatics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge