Generalized Kernel Inducing Points by Duality Gap for Dataset Distillation

We propose Duality Gap KIP (DGKIP), an extension of the Kernel Inducing Points (KIP) method for dataset distillation. While existing dataset distillation methods often rely on bi-level optimization, DGKIP eliminates the need for such optimization by leveraging duality theory in convex programming. The KIP method has been introduced as a way to avoid bi-level optimization; however, it is limited to the squared loss and does not support other loss functions (e.g., cross-entropy or hinge loss) that are more suitable for classification tasks. DGKIP addresses this limitation by exploiting an upper bound on parameter changes after dataset distillation using the duality gap, enabling its application to a wider range of loss functions. We also characterize theoretical properties of DGKIP by providing upper bounds on the test error and prediction consistency after dataset distillation. Experimental results on standard benchmarks such as MNIST and CIFAR-10 demonstrate that DGKIP retains the efficiency of KIP while offering broader applicability and robust performance.

Distributionally Robust Coreset Selection under Covariate Shift

Coreset selection, which involves selecting a small subset from an existing training dataset, is an approach to reducing training data, and various approaches have been proposed for this method. In practical situations where these methods are employed, it is often the case that the data distributions differ between the development phase and the deployment phase, with the latter being unknown. Thus, it is challenging to select an effective subset of training data that performs well across all deployment scenarios. We therefore propose Distributionally Robust Coreset Selection (DRCS). DRCS theoretically derives an estimate of the upper bound for the worst-case test error, assuming that the future covariate distribution may deviate within a defined range from the training distribution. Furthermore, by selecting instances in a way that suppresses the estimate of the upper bound for the worst-case test error, DRCS achieves distributionally robust training instance selection. This study is primarily applicable to convex training computation, but we demonstrate that it can also be applied to deep learning under appropriate approximations. In this paper, we focus on covariate shift, a type of data distribution shift, and demonstrate the effectiveness of DRCS through experiments.

Distributionally Robust Safe Sample Screening

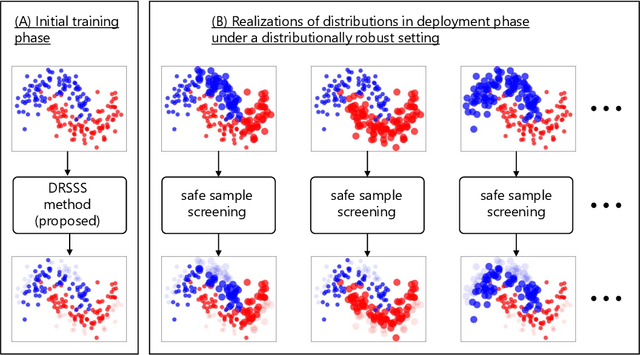
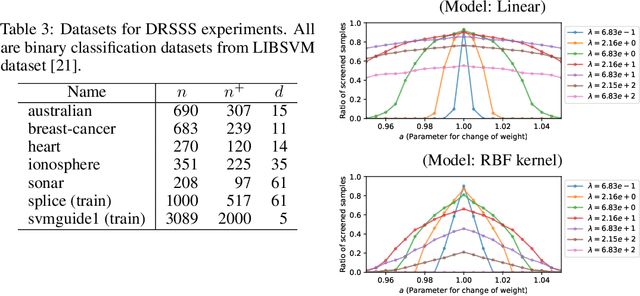
In this study, we propose a machine learning method called Distributionally Robust Safe Sample Screening (DRSSS). DRSSS aims to identify unnecessary training samples, even when the distribution of the training samples changes in the future. To achieve this, we effectively combine the distributionally robust (DR) paradigm, which aims to enhance model robustness against variations in data distribution, with the safe sample screening (SSS), which identifies unnecessary training samples prior to model training. Since we need to consider an infinite number of scenarios regarding changes in the distribution, we applied SSS because it does not require model training after the change of the distribution. In this paper, we employed the covariate shift framework to represent the distribution of training samples and reformulated the DR covariate-shift problem as a weighted empirical risk minimization problem, where the weights are subject to uncertainty within a predetermined range. By extending the existing SSS technique to accommodate this weight uncertainty, the DRSSS method is capable of reliably identifying unnecessary samples under any future distribution within a specified range. We provide a theoretical guarantee for the DRSSS method and validate its performance through numerical experiments on both synthetic and real-world datasets.

Distributionally Robust Safe Screening

In this study, we propose a method Distributionally Robust Safe Screening (DRSS), for identifying unnecessary samples and features within a DR covariate shift setting. This method effectively combines DR learning, a paradigm aimed at enhancing model robustness against variations in data distribution, with safe screening (SS), a sparse optimization technique designed to identify irrelevant samples and features prior to model training. The core concept of the DRSS method involves reformulating the DR covariate-shift problem as a weighted empirical risk minimization problem, where the weights are subject to uncertainty within a predetermined range. By extending the SS technique to accommodate this weight uncertainty, the DRSS method is capable of reliably identifying unnecessary samples and features under any future distribution within a specified range. We provide a theoretical guarantee of the DRSS method and validate its performance through numerical experiments on both synthetic and real-world datasets.