Aoyama Tatsuya
Distributionally Robust Active Learning for Gaussian Process Regression
Feb 24, 2025Abstract:Gaussian process regression (GPR) or kernel ridge regression is a widely used and powerful tool for nonlinear prediction. Therefore, active learning (AL) for GPR, which actively collects data labels to achieve an accurate prediction with fewer data labels, is an important problem. However, existing AL methods do not theoretically guarantee prediction accuracy for target distribution. Furthermore, as discussed in the distributionally robust learning literature, specifying the target distribution is often difficult. Thus, this paper proposes two AL methods that effectively reduce the worst-case expected error for GPR, which is the worst-case expectation in target distribution candidates. We show an upper bound of the worst-case expected squared error, which suggests that the error will be arbitrarily small by a finite number of data labels under mild conditions. Finally, we demonstrate the effectiveness of the proposed methods through synthetic and real-world datasets.
Distributionally Robust Safe Sample Screening
Jun 10, 2024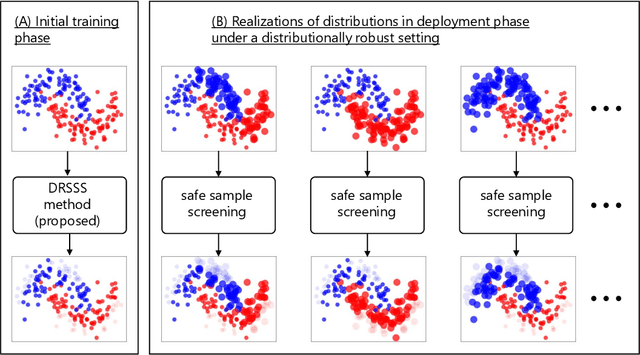


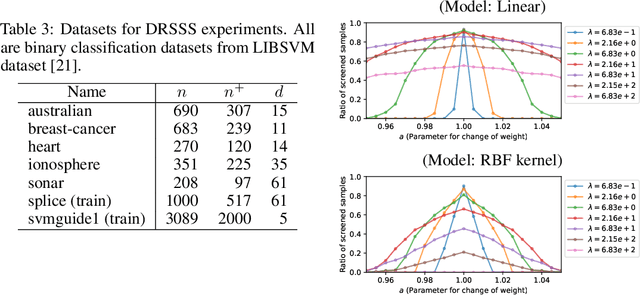
Abstract:In this study, we propose a machine learning method called Distributionally Robust Safe Sample Screening (DRSSS). DRSSS aims to identify unnecessary training samples, even when the distribution of the training samples changes in the future. To achieve this, we effectively combine the distributionally robust (DR) paradigm, which aims to enhance model robustness against variations in data distribution, with the safe sample screening (SSS), which identifies unnecessary training samples prior to model training. Since we need to consider an infinite number of scenarios regarding changes in the distribution, we applied SSS because it does not require model training after the change of the distribution. In this paper, we employed the covariate shift framework to represent the distribution of training samples and reformulated the DR covariate-shift problem as a weighted empirical risk minimization problem, where the weights are subject to uncertainty within a predetermined range. By extending the existing SSS technique to accommodate this weight uncertainty, the DRSSS method is capable of reliably identifying unnecessary samples under any future distribution within a specified range. We provide a theoretical guarantee for the DRSSS method and validate its performance through numerical experiments on both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge