An $(ε,δ)$-accurate level set estimation with a stopping criterion
Paper and Code
Mar 26, 2025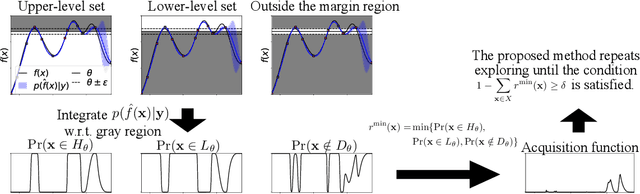
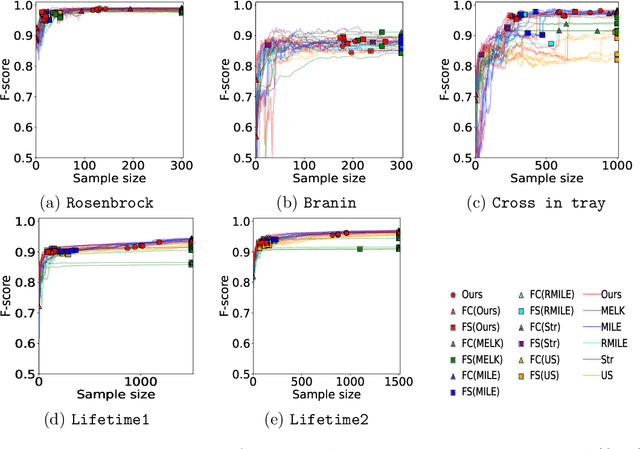
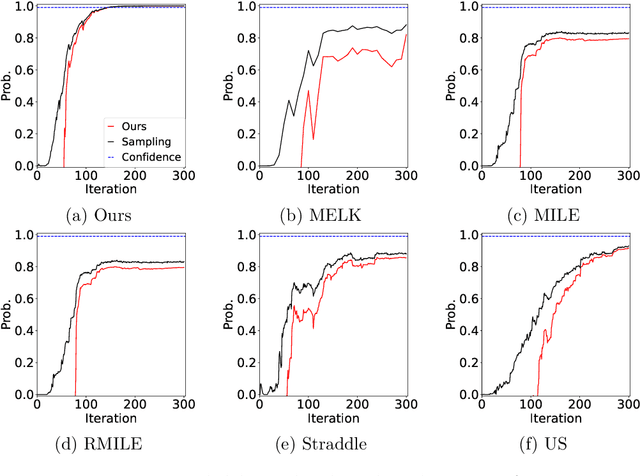
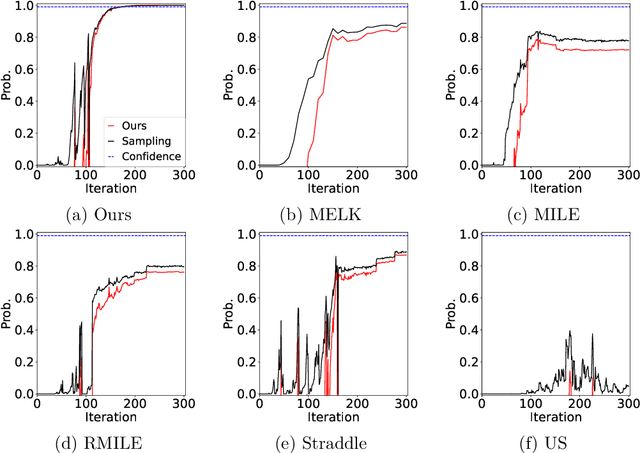
The level set estimation problem seeks to identify regions within a set of candidate points where an unknown and costly to evaluate function's value exceeds a specified threshold, providing an efficient alternative to exhaustive evaluations of function values. Traditional methods often use sequential optimization strategies to find $\epsilon$-accurate solutions, which permit a margin around the threshold contour but frequently lack effective stopping criteria, leading to excessive exploration and inefficiencies. This paper introduces an acquisition strategy for level set estimation that incorporates a stopping criterion, ensuring the algorithm halts when further exploration is unlikely to yield improvements, thereby reducing unnecessary function evaluations. We theoretically prove that our method satisfies $\epsilon$-accuracy with a confidence level of $1 - \delta$, addressing a key gap in existing approaches. Furthermore, we show that this also leads to guarantees on the lower bounds of performance metrics such as F-score. Numerical experiments demonstrate that the proposed acquisition function achieves comparable precision to existing methods while confirming that the stopping criterion effectively terminates the algorithm once adequate exploration is completed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge