Scaling-based Data Augmentation for Generative Models and its Theoretical Extension

This paper studies stable learning methods for generative models that enable high-quality data generation. Noise injection is commonly used to stabilize learning. However, selecting a suitable noise distribution is challenging. Diffusion-GAN, a recently developed method, addresses this by using the diffusion process with a timestep-dependent discriminator. We investigate Diffusion-GAN and reveal that data scaling is a key component for stable learning and high-quality data generation. Building on our findings, we propose a learning algorithm, Scale-GAN, that uses data scaling and variance-based regularization. Furthermore, we theoretically prove that data scaling controls the bias-variance trade-off of the estimation error bound. As a theoretical extension, we consider GAN with invertible data augmentations. Comparative evaluations on benchmark datasets demonstrate the effectiveness of our method in improving stability and accuracy.

Robust Estimation for Kernel Exponential Families with Smoothed Total Variation Distances

In statistical inference, we commonly assume that samples are independent and identically distributed from a probability distribution included in a pre-specified statistical model. However, such an assumption is often violated in practice. Even an unexpected extreme sample called an {\it outlier} can significantly impact classical estimators. Robust statistics studies how to construct reliable statistical methods that efficiently work even when the ideal assumption is violated. Recently, some works revealed that robust estimators such as Tukey's median are well approximated by the generative adversarial net (GAN), a popular learning method for complex generative models using neural networks. GAN is regarded as a learning method using integral probability metrics (IPM), which is a discrepancy measure for probability distributions. In most theoretical analyses of Tukey's median and its GAN-based approximation, however, the Gaussian or elliptical distribution is assumed as the statistical model. In this paper, we explore the application of GAN-like estimators to a general class of statistical models. As the statistical model, we consider the kernel exponential family that includes both finite and infinite-dimensional models. To construct a robust estimator, we propose the smoothed total variation (STV) distance as a class of IPMs. Then, we theoretically investigate the robustness properties of the STV-based estimators. Our analysis reveals that the STV-based estimator is robust against the distribution contamination for the kernel exponential family. Furthermore, we analyze the prediction accuracy of a Monte Carlo approximation method, which circumvents the computational difficulty of the normalization constant.

Robust VAEs via Generating Process of Noise Augmented Data

Advancing defensive mechanisms against adversarial attacks in generative models is a critical research topic in machine learning. Our study focuses on a specific type of generative models - Variational Auto-Encoders (VAEs). Contrary to common beliefs and existing literature which suggest that noise injection towards training data can make models more robust, our preliminary experiments revealed that naive usage of noise augmentation technique did not substantially improve VAE robustness. In fact, it even degraded the quality of learned representations, making VAEs more susceptible to adversarial perturbations. This paper introduces a novel framework that enhances robustness by regularizing the latent space divergence between original and noise-augmented data. Through incorporating a paired probabilistic prior into the standard variational lower bound, our method significantly boosts defense against adversarial attacks. Our empirical evaluations demonstrate that this approach, termed Robust Augmented Variational Auto-ENcoder (RAVEN), yields superior performance in resisting adversarial inputs on widely-recognized benchmark datasets.

A Convex Framework for Confounding Robust Inference

We study policy evaluation of offline contextual bandits subject to unobserved confounders. Sensitivity analysis methods are commonly used to estimate the policy value under the worst-case confounding over a given uncertainty set. However, existing work often resorts to some coarse relaxation of the uncertainty set for the sake of tractability, leading to overly conservative estimation of the policy value. In this paper, we propose a general estimator that provides a sharp lower bound of the policy value using convex programming. The generality of our estimator enables various extensions such as sensitivity analysis with f-divergence, model selection with cross validation and information criterion, and robust policy learning with the sharp lower bound. Furthermore, our estimation method can be reformulated as an empirical risk minimization problem thanks to the strong duality, which enables us to provide strong theoretical guarantees of the proposed estimator using techniques of the M-estimation.

Denoising Cosine Similarity: A Theory-Driven Approach for Efficient Representation Learning

Representation learning has been increasing its impact on the research and practice of machine learning, since it enables to learn representations that can apply to various downstream tasks efficiently. However, recent works pay little attention to the fact that real-world datasets used during the stage of representation learning are commonly contaminated by noise, which can degrade the quality of learned representations. This paper tackles the problem to learn robust representations against noise in a raw dataset. To this end, inspired by recent works on denoising and the success of the cosine-similarity-based objective functions in representation learning, we propose the denoising Cosine-Similarity (dCS) loss. The dCS loss is a modified cosine-similarity loss and incorporates a denoising property, which is supported by both our theoretical and empirical findings. To make the dCS loss implementable, we also construct the estimators of the dCS loss with statistical guarantees. Finally, we empirically show the efficiency of the dCS loss over the baseline objective functions in vision and speech domains.

Towards Understanding the Mechanism of Contrastive Learning via Similarity Structure: A Theoretical Analysis

Contrastive learning is an efficient approach to self-supervised representation learning. Although recent studies have made progress in the theoretical understanding of contrastive learning, the investigation of how to characterize the clusters of the learned representations is still limited. In this paper, we aim to elucidate the characterization from theoretical perspectives. To this end, we consider a kernel-based contrastive learning framework termed Kernel Contrastive Learning (KCL), where kernel functions play an important role when applying our theoretical results to other frameworks. We introduce a formulation of the similarity structure of learned representations by utilizing a statistical dependency viewpoint. We investigate the theoretical properties of the kernel-based contrastive loss via this formulation. We first prove that the formulation characterizes the structure of representations learned with the kernel-based contrastive learning framework. We show a new upper bound of the classification error of a downstream task, which explains that our theory is consistent with the empirical success of contrastive learning. We also establish a generalization error bound of KCL. Finally, we show a guarantee for the generalization ability of KCL to the downstream classification task via a surrogate bound.

Deep Clustering with a Constraint for Topological Invariance based on Symmetric InfoNCE

We consider the scenario of deep clustering, in which the available prior knowledge is limited. In this scenario, few existing state-of-the-art deep clustering methods can perform well for both non-complex topology and complex topology datasets. To address the problem, we propose a constraint utilizing symmetric InfoNCE, which helps an objective of deep clustering method in the scenario train the model so as to be efficient for not only non-complex topology but also complex topology datasets. Additionally, we provide several theoretical explanations of the reason why the constraint can enhances performance of deep clustering methods. To confirm the effectiveness of the proposed constraint, we introduce a deep clustering method named MIST, which is a combination of an existing deep clustering method and our constraint. Our numerical experiments via MIST demonstrate that the constraint is effective. In addition, MIST outperforms other state-of-the-art deep clustering methods for most of the commonly used ten benchmark datasets.

Learning Domain Invariant Representations by Joint Wasserstein Distance Minimization

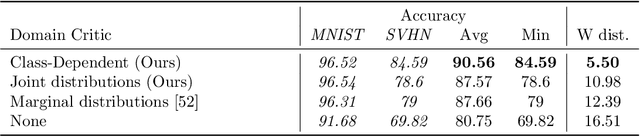
Domain shifts in the training data are common in practical applications of machine learning, they occur for instance when the data is coming from different sources. Ideally, a ML model should work well independently of these shifts, for example, by learning a domain-invariant representation. Moreover, privacy concerns regarding the source also require a domain-invariant representation. In this work, we provide theoretical results that link domain invariant representations -- measured by the Wasserstein distance on the joint distributions -- to a practical semi-supervised learning objective based on a cross-entropy classifier and a novel domain critic. Quantitative experiments demonstrate that the proposed approach is indeed able to practically learn such an invariant representation (between two domains), and the latter also supports models with higher predictive accuracy on both domains, comparing favorably to existing techniques.

Robust modal regression with direct log-density derivative estimation

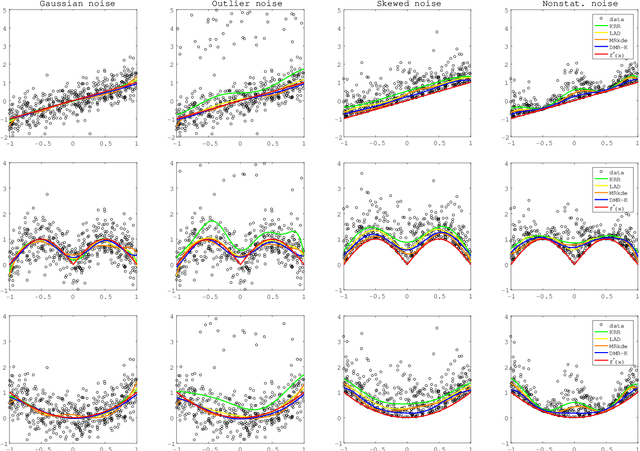
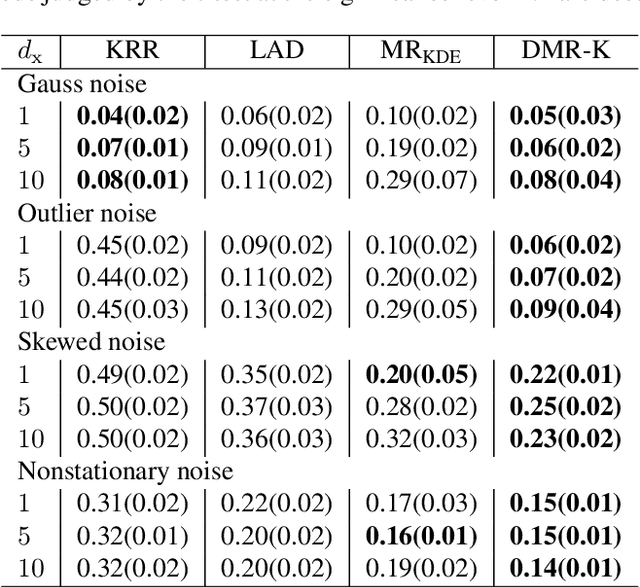
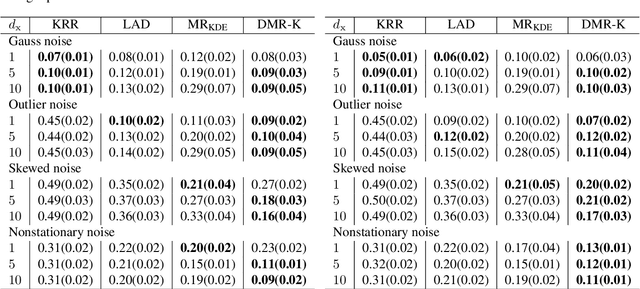
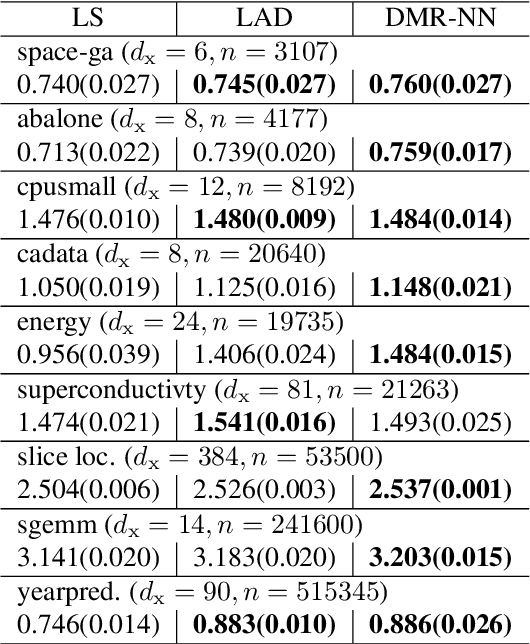
Modal regression is aimed at estimating the global mode (i.e., global maximum) of the conditional density function of the output variable given input variables, and has led to regression methods robust against heavy-tailed or skewed noises. The conditional mode is often estimated through maximization of the modal regression risk (MRR). In order to apply a gradient method for the maximization, the fundamental challenge is accurate approximation of the gradient of MRR, not MRR itself. To overcome this challenge, in this paper, we take a novel approach of directly approximating the gradient of MRR. To approximate the gradient, we develop kernelized and neural-network-based versions of the least-squares log-density derivative estimator, which directly approximates the derivative of the log-density without density estimation. With direct approximation of the MRR gradient, we first propose a modal regression method with kernels, and derive a new parameter update rule based on a fixed-point method. Then, the derived update rule is theoretically proved to have a monotonic hill-climbing property towards the conditional mode. Furthermore, we indicate that our approach of directly approximating the gradient is compatible with recent sophisticated stochastic gradient methods (e.g., Adam), and then propose another modal regression method based on neural networks. Finally, the superior performance of the proposed methods is demonstrated on various artificial and benchmark datasets.

Estimating Density Models with Complex Truncation Boundaries

Truncated densities are probability density functions defined on truncated input domains. These densities share the same parametric form with their non-truncated counterparts up to a normalization term. However, normalization terms usually cannot be obtained in closed form for these distributions, due to complicated truncation domains. Score Matching is a powerful tool for fitting parameters in unnormalized models. However, it cannot be straightforwardly applied here as boundary conditions used to derive a tractable objective are usually not satisfied by truncated distributions. In this paper, we propose a maximally weighted Score Matching objective function which takes the geometry of the truncation boundary into account when fitting unnormalized density models. We show the weighting function that maximizes the objective function can be constructed easily and the boundary conditions for deriving a tradable objective are satisfied. Experiments on toy datasets and Chicago crime dataset show promising results.