On the Parallel Complexity of Multilevel Monte Carlo in Stochastic Gradient Descent

In the stochastic gradient descent (SGD) for sequential simulations such as the neural stochastic differential equations, the Multilevel Monte Carlo (MLMC) method is known to offer better theoretical computational complexity compared to the naive Monte Carlo approach. However, in practice, MLMC scales poorly on massively parallel computing platforms such as modern GPUs, because of its large parallel complexity which is equivalent to that of the naive Monte Carlo method. To cope with this issue, we propose the delayed MLMC gradient estimator that drastically reduces the parallel complexity of MLMC by recycling previously computed gradient components from earlier steps of SGD. The proposed estimator provably reduces the average parallel complexity per iteration at the cost of a slightly worse per-iteration convergence rate. In our numerical experiments, we use an example of deep hedging to demonstrate the superior parallel complexity of our method compared to the standard MLMC in SGD.

A Convex Framework for Confounding Robust Inference

We study policy evaluation of offline contextual bandits subject to unobserved confounders. Sensitivity analysis methods are commonly used to estimate the policy value under the worst-case confounding over a given uncertainty set. However, existing work often resorts to some coarse relaxation of the uncertainty set for the sake of tractability, leading to overly conservative estimation of the policy value. In this paper, we propose a general estimator that provides a sharp lower bound of the policy value using convex programming. The generality of our estimator enables various extensions such as sensitivity analysis with f-divergence, model selection with cross validation and information criterion, and robust policy learning with the sharp lower bound. Furthermore, our estimation method can be reformulated as an empirical risk minimization problem thanks to the strong duality, which enables us to provide strong theoretical guarantees of the proposed estimator using techniques of the M-estimation.

Kernel Conditional Moment Constraints for Confounding Robust Inference

We study policy evaluation of offline contextual bandits subject to unobserved confounders. Sensitivity analysis methods are commonly used to estimate the policy value under the worst-case confounding over a given uncertainty set. However, existing work often resorts to some coarse relaxation of the uncertainty set for the sake of tractability, leading to overly conservative estimation of the policy value. In this paper, we propose a general estimator that provides a sharp lower bound of the policy value. It can be shown that our estimator contains the recently proposed sharp estimator by Dorn and Guo (2022) as a special case, and our method enables a novel extension of the classical marginal sensitivity model using f-divergence. To construct our estimator, we leverage the kernel method to obtain a tractable approximation to the conditional moment constraints, which traditional non-sharp estimators failed to take into account. In the theoretical analysis, we provide a condition for the choice of the kernel which guarantees no specification error that biases the lower bound estimation. Furthermore, we provide consistency guarantees of policy evaluation and learning. In the experiments with synthetic and real-world data, we demonstrate the effectiveness of the proposed method.

Efficient Debiased Variational Bayes by Multilevel Monte Carlo Methods

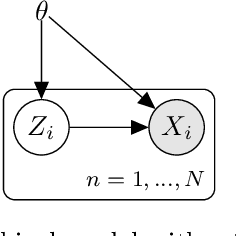
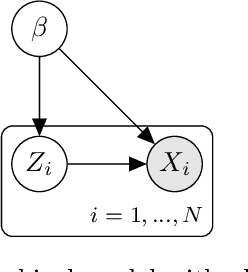
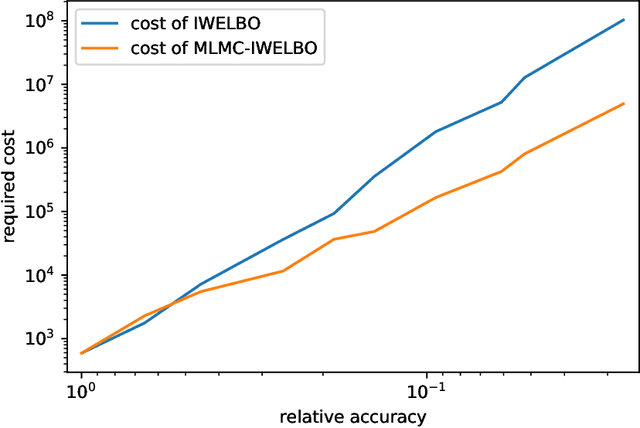
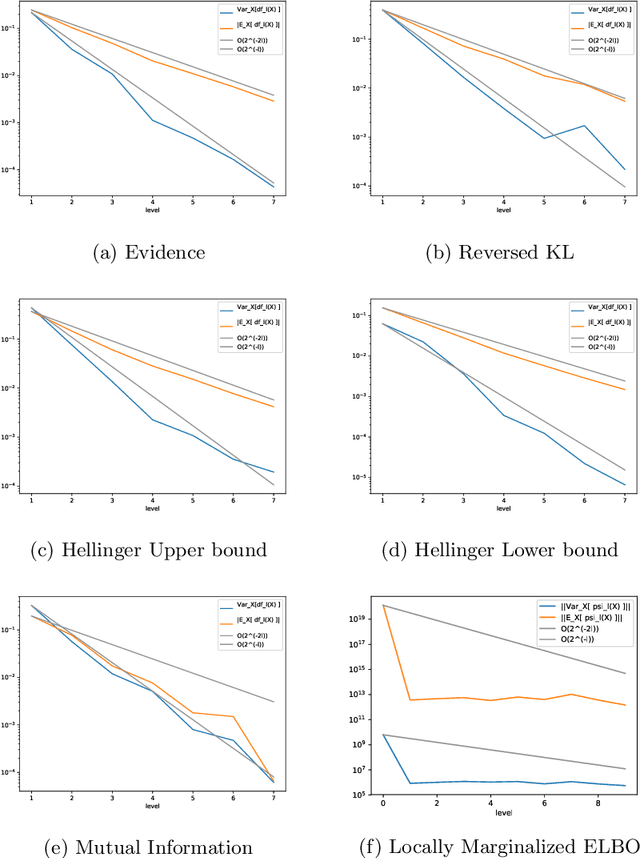
Variational Bayes is a method to find a good approximation of the posterior probability distribution of latent variables from a parametric family of distributions. The evidence lower bound (ELBO), which is nothing but the model evidence minus the Kullback-Leibler divergence, has been commonly used as a quality measure in the optimization process. However, the model evidence itself has been considered computationally intractable since it is expressed as a nested expectation with an outer expectation with respect to the training dataset and an inner conditional expectation with respect to latent variables. Similarly, if the Kullback-Leibler divergence is replaced with another divergence metric, the corresponding lower bound on the model evidence is often given by such a nested expectation. The standard (nested) Monte Carlo method can be used to estimate such quantities, whereas the resulting estimate is biased and the variance is often quite large. Recently the authors provided an unbiased estimator of the model evidence with small variance by applying the idea from multilevel Monte Carlo (MLMC) methods. In this article, we give more examples involving nested expectations in the context of variational Bayes where MLMC methods can help construct low-variance unbiased estimators, and provide numerical results which demonstrate the effectiveness of our proposed estimators.

Multilevel Monte Carlo estimation of log marginal likelihood

In this short note we provide an unbiased multilevel Monte Carlo estimator of the log marginal likelihood and discuss its application to variational Bayes.