Efficient Debiased Variational Bayes by Multilevel Monte Carlo Methods

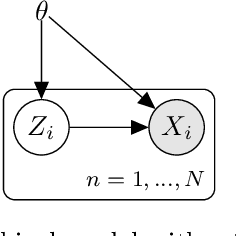
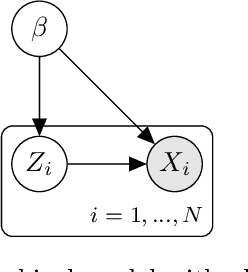
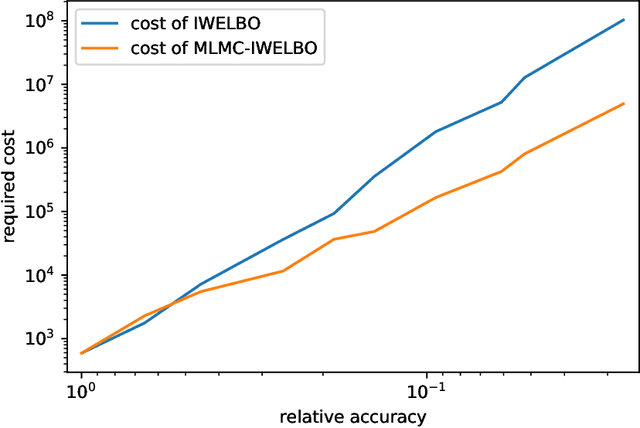
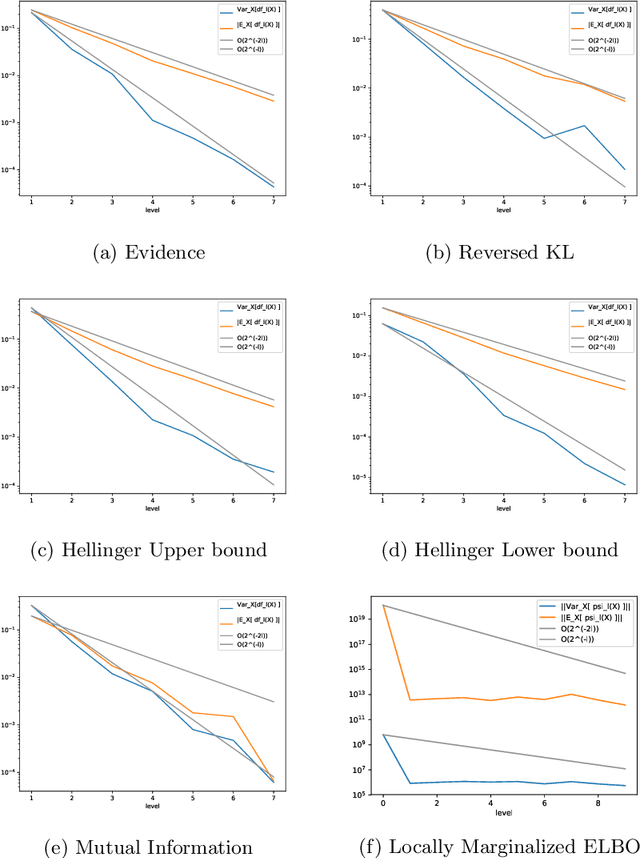
Variational Bayes is a method to find a good approximation of the posterior probability distribution of latent variables from a parametric family of distributions. The evidence lower bound (ELBO), which is nothing but the model evidence minus the Kullback-Leibler divergence, has been commonly used as a quality measure in the optimization process. However, the model evidence itself has been considered computationally intractable since it is expressed as a nested expectation with an outer expectation with respect to the training dataset and an inner conditional expectation with respect to latent variables. Similarly, if the Kullback-Leibler divergence is replaced with another divergence metric, the corresponding lower bound on the model evidence is often given by such a nested expectation. The standard (nested) Monte Carlo method can be used to estimate such quantities, whereas the resulting estimate is biased and the variance is often quite large. Recently the authors provided an unbiased estimator of the model evidence with small variance by applying the idea from multilevel Monte Carlo (MLMC) methods. In this article, we give more examples involving nested expectations in the context of variational Bayes where MLMC methods can help construct low-variance unbiased estimators, and provide numerical results which demonstrate the effectiveness of our proposed estimators.