Constructing unbiased gradient estimators with finite variance for conditional stochastic optimization

We study stochastic gradient descent for solving conditional stochastic optimization problems, in which an objective to be minimized is given by a parametric nested expectation with an outer expectation taken with respect to one random variable and an inner conditional expectation with respect to the other random variable. The gradient of such a parametric nested expectation is again expressed as a nested expectation, which makes it hard for the standard nested Monte Carlo estimator to be unbiased. In this paper, we show under some conditions that a multilevel Monte Carlo gradient estimator is unbiased and has finite variance and finite expected computational cost, so that the standard theory from stochastic optimization for a parametric (non-nested) expectation directly applies. We also discuss a special case for which yet another unbiased gradient estimator with finite variance and cost can be constructed.

Unbiased MLMC stochastic gradient-based optimization of Bayesian experimental designs

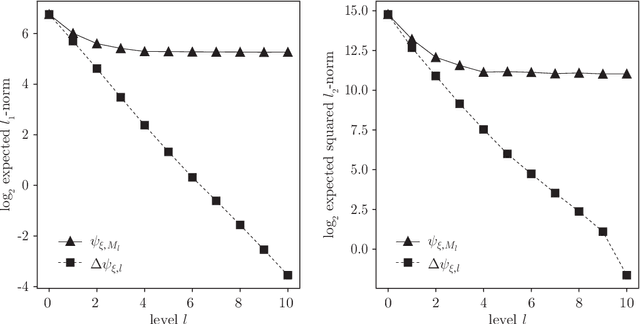
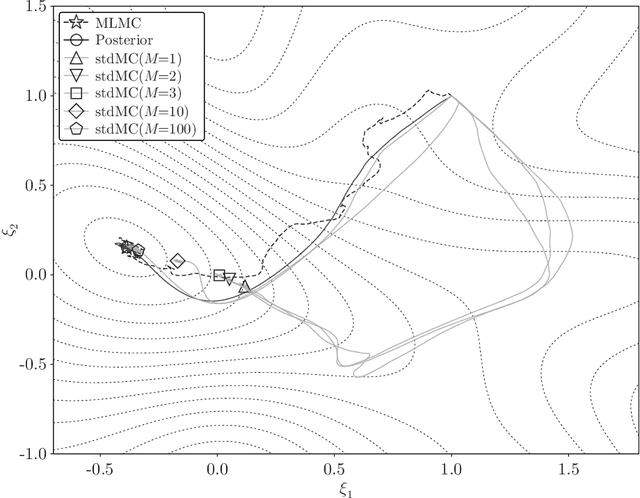
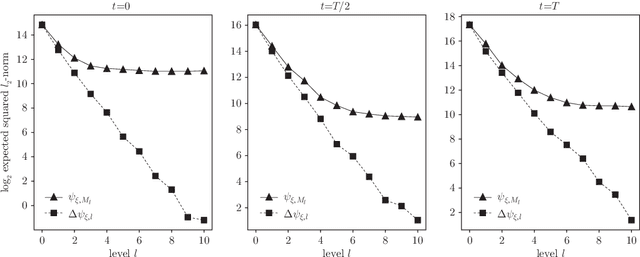
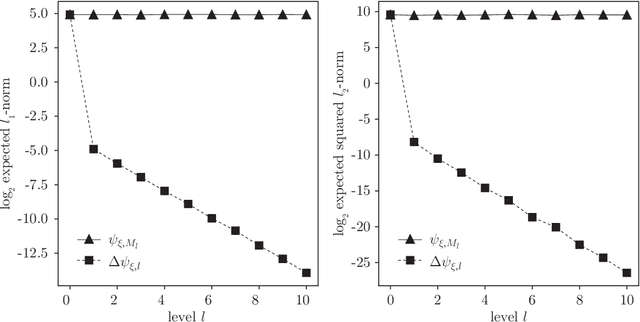
In this paper we propose an efficient stochastic optimization algorithm to search for Bayesian experimental designs such that the expected information gain is maximized. The gradient of the expected information gain with respect to experimental design parameters is given by a nested expectation, for which the standard Monte Carlo method using a fixed number of inner samples yields a biased estimator. In this paper, applying the idea of randomized multilevel Monte Carlo methods, we introduce an unbiased Monte Carlo estimator for the gradient of the expected information gain with finite expected squared $\ell_2$-norm and finite expected computational cost per sample. Our unbiased estimator can be combined well with stochastic gradient descent algorithms, which results in our proposal of an optimization algorithm to search for an optimal Bayesian experimental design. Numerical experiments confirm that our proposed algorithm works well not only for a simple test problem but also for a more realistic pharmacokinetic problem.

Efficient Debiased Variational Bayes by Multilevel Monte Carlo Methods

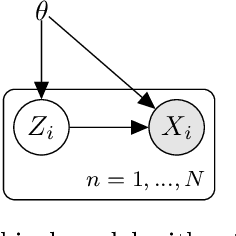
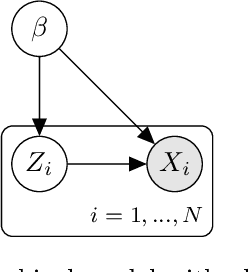
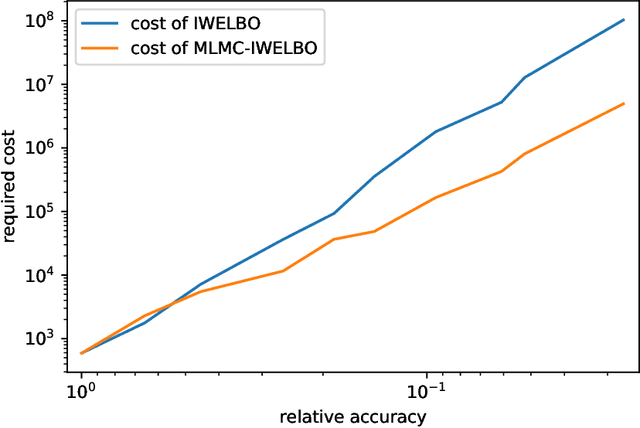
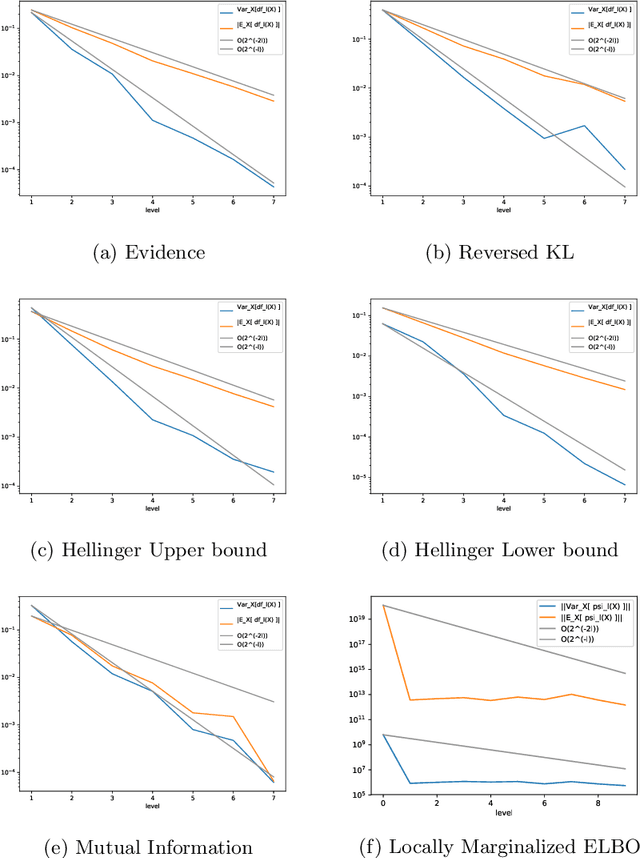
Variational Bayes is a method to find a good approximation of the posterior probability distribution of latent variables from a parametric family of distributions. The evidence lower bound (ELBO), which is nothing but the model evidence minus the Kullback-Leibler divergence, has been commonly used as a quality measure in the optimization process. However, the model evidence itself has been considered computationally intractable since it is expressed as a nested expectation with an outer expectation with respect to the training dataset and an inner conditional expectation with respect to latent variables. Similarly, if the Kullback-Leibler divergence is replaced with another divergence metric, the corresponding lower bound on the model evidence is often given by such a nested expectation. The standard (nested) Monte Carlo method can be used to estimate such quantities, whereas the resulting estimate is biased and the variance is often quite large. Recently the authors provided an unbiased estimator of the model evidence with small variance by applying the idea from multilevel Monte Carlo (MLMC) methods. In this article, we give more examples involving nested expectations in the context of variational Bayes where MLMC methods can help construct low-variance unbiased estimators, and provide numerical results which demonstrate the effectiveness of our proposed estimators.

Multilevel Monte Carlo estimation of log marginal likelihood

In this short note we provide an unbiased multilevel Monte Carlo estimator of the log marginal likelihood and discuss its application to variational Bayes.