Constructing unbiased gradient estimators with finite variance for conditional stochastic optimization

We study stochastic gradient descent for solving conditional stochastic optimization problems, in which an objective to be minimized is given by a parametric nested expectation with an outer expectation taken with respect to one random variable and an inner conditional expectation with respect to the other random variable. The gradient of such a parametric nested expectation is again expressed as a nested expectation, which makes it hard for the standard nested Monte Carlo estimator to be unbiased. In this paper, we show under some conditions that a multilevel Monte Carlo gradient estimator is unbiased and has finite variance and finite expected computational cost, so that the standard theory from stochastic optimization for a parametric (non-nested) expectation directly applies. We also discuss a special case for which yet another unbiased gradient estimator with finite variance and cost can be constructed.

Unbiased MLMC stochastic gradient-based optimization of Bayesian experimental designs

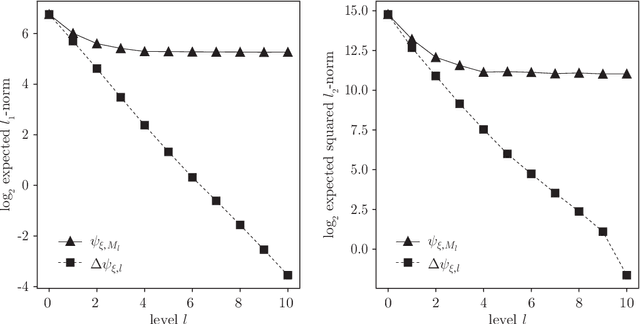
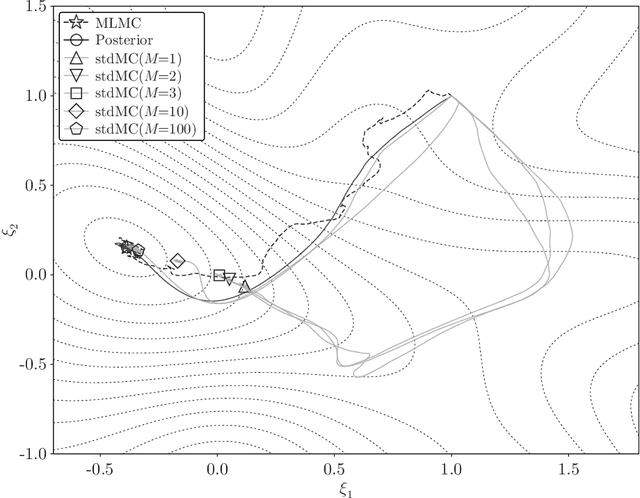
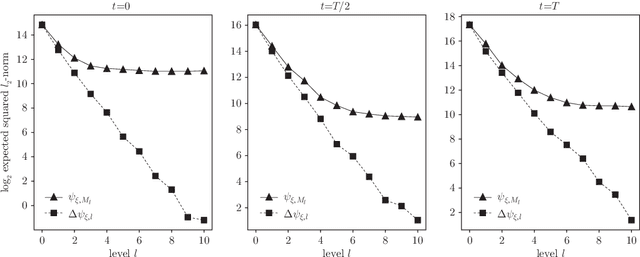
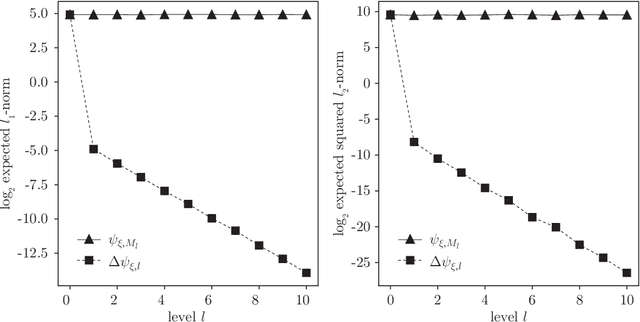
In this paper we propose an efficient stochastic optimization algorithm to search for Bayesian experimental designs such that the expected information gain is maximized. The gradient of the expected information gain with respect to experimental design parameters is given by a nested expectation, for which the standard Monte Carlo method using a fixed number of inner samples yields a biased estimator. In this paper, applying the idea of randomized multilevel Monte Carlo methods, we introduce an unbiased Monte Carlo estimator for the gradient of the expected information gain with finite expected squared $\ell_2$-norm and finite expected computational cost per sample. Our unbiased estimator can be combined well with stochastic gradient descent algorithms, which results in our proposal of an optimization algorithm to search for an optimal Bayesian experimental design. Numerical experiments confirm that our proposed algorithm works well not only for a simple test problem but also for a more realistic pharmacokinetic problem.