Identifiability of a statistical model with two latent vectors: Importance of the dimensionality relation and application to graph embedding

Identifiability of statistical models is a key notion in unsupervised representation learning. Recent work of nonlinear independent component analysis (ICA) employs auxiliary data and has established identifiable conditions. This paper proposes a statistical model of two latent vectors with single auxiliary data generalizing nonlinear ICA, and establishes various identifiability conditions. Unlike previous work, the two latent vectors in the proposed model can have arbitrary dimensions, and this property enables us to reveal an insightful dimensionality relation among two latent vectors and auxiliary data in identifiability conditions. Furthermore, surprisingly, we prove that the indeterminacies of the proposed model has the same as \emph{linear} ICA under certain conditions: The elements in the latent vector can be recovered up to their permutation and scales. Next, we apply the identifiability theory to a statistical model for graph data. As a result, one of the identifiability conditions includes an appealing implication: Identifiability of the statistical model could depend on the maximum value of link weights in graph data. Then, we propose a practical method for identifiable graph embedding. Finally, we numerically demonstrate that the proposed method well-recovers the latent vectors and model identifiability clearly depends on the maximum value of link weights, which supports the implication of our theoretical results

A unified view for unsupervised representation learning with density ratio estimation: Maximization of mutual information, nonlinear ICA and nonlinear subspace estimation

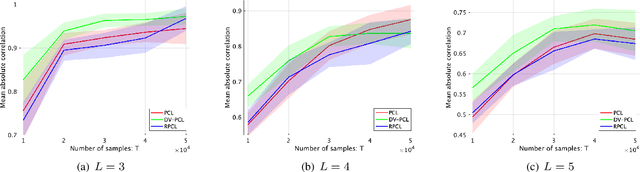
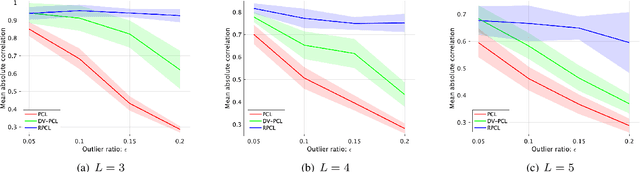
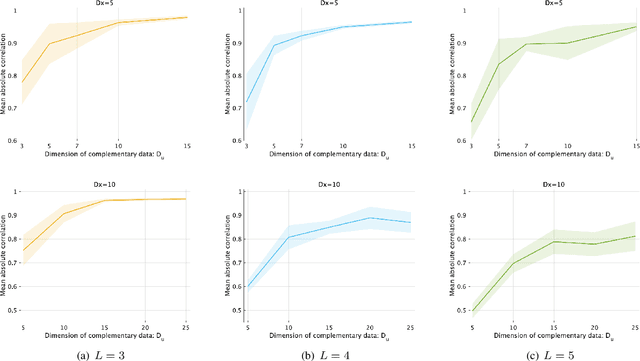
Unsupervised representation learning is one of the most important problems in machine learning. Recent promising methods are based on contrastive learning. However, contrastive learning often relies on heuristic ideas, and therefore it is not easy to understand what contrastive learning is doing. This paper emphasizes that density ratio estimation is a promising goal for unsupervised representation learning, and promotes understanding to contrastive learning. Our primal contribution is to theoretically show that density ratio estimation unifies three frameworks for unsupervised representation learning: Maximization of mutual information (MI), nonlinear independent component analysis (ICA) and a novel framework for estimation of a lower-dimensional nonlinear subspace proposed in this paper. This unified view clarifies under what conditions contrastive learning can be regarded as maximizing MI, performing nonlinear ICA or estimating the lower-dimensional nonlinear subspace in the proposed framework. Furthermore, we also make theoretical contributions in each of the three frameworks: We show that MI can be maximized through density ratio estimation under certain conditions, while our analysis for nonlinear ICA reveals a novel insight for recovery of the latent source components, which is clearly supported by numerical experiments. In addition, some theoretical conditions are also established to estimate a nonlinear subspace in the proposed framework. Based on the unified view, we propose two practical methods for unsupervised representation learning through density ratio estimation: The first method is an outlier-robust method for representation learning, while the second one is a sample-efficient nonlinear ICA method. Finally, we numerically demonstrate usefulness of the proposed methods in nonlinear ICA and through application to a downstream task for classification.

Robust contrastive learning and nonlinear ICA in the presence of outliers

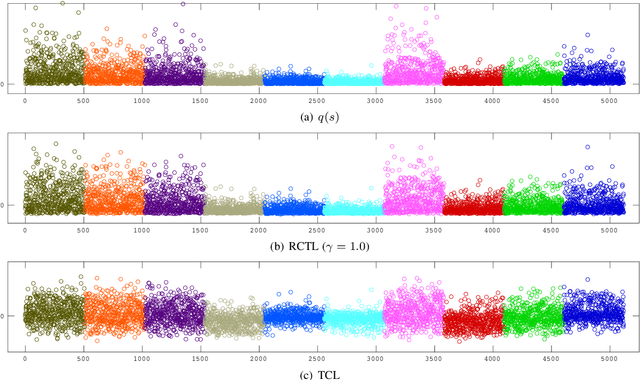
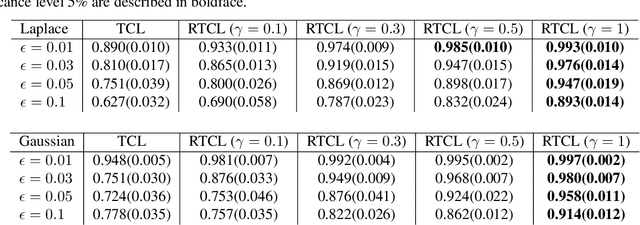
Nonlinear independent component analysis (ICA) is a general framework for unsupervised representation learning, and aimed at recovering the latent variables in data. Recent practical methods perform nonlinear ICA by solving a series of classification problems based on logistic regression. However, it is well-known that logistic regression is vulnerable to outliers, and thus the performance can be strongly weakened by outliers. In this paper, we first theoretically analyze nonlinear ICA models in the presence of outliers. Our analysis implies that estimation in nonlinear ICA can be seriously hampered when outliers exist on the tails of the (noncontaminated) target density, which happens in a typical case of contamination by outliers. We develop two robust nonlinear ICA methods based on the {\gamma}-divergence, which is a robust alternative to the KL-divergence in logistic regression. The proposed methods are shown to have desired robustness properties in the context of nonlinear ICA. We also experimentally demonstrate that the proposed methods are very robust and outperform existing methods in the presence of outliers. Finally, the proposed method is applied to ICA-based causal discovery and shown to find a plausible causal relationship on fMRI data.

Robust modal regression with direct log-density derivative estimation

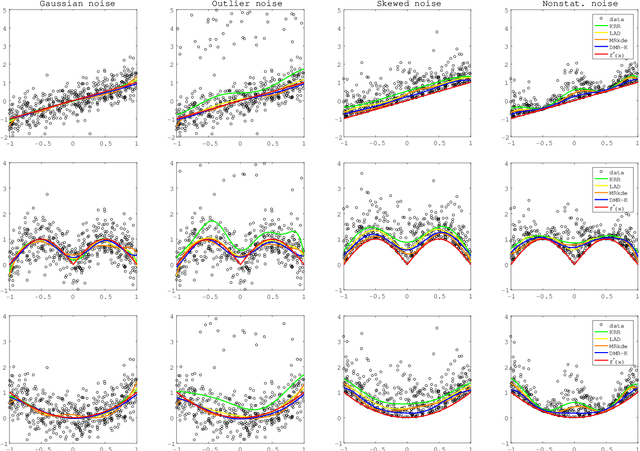
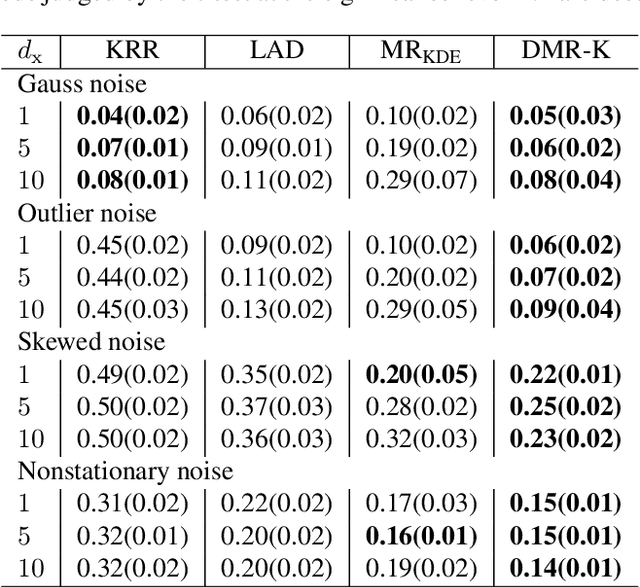
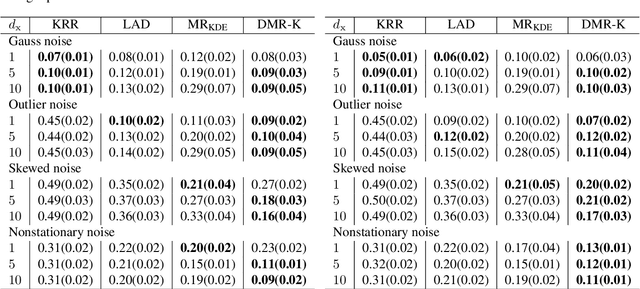
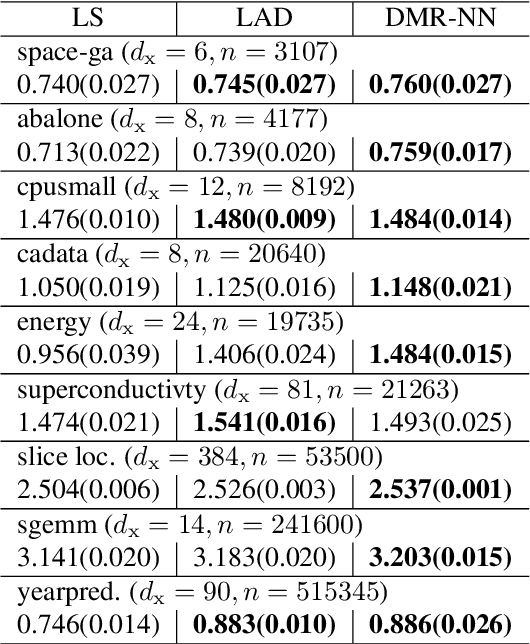
Modal regression is aimed at estimating the global mode (i.e., global maximum) of the conditional density function of the output variable given input variables, and has led to regression methods robust against heavy-tailed or skewed noises. The conditional mode is often estimated through maximization of the modal regression risk (MRR). In order to apply a gradient method for the maximization, the fundamental challenge is accurate approximation of the gradient of MRR, not MRR itself. To overcome this challenge, in this paper, we take a novel approach of directly approximating the gradient of MRR. To approximate the gradient, we develop kernelized and neural-network-based versions of the least-squares log-density derivative estimator, which directly approximates the derivative of the log-density without density estimation. With direct approximation of the MRR gradient, we first propose a modal regression method with kernels, and derive a new parameter update rule based on a fixed-point method. Then, the derived update rule is theoretically proved to have a monotonic hill-climbing property towards the conditional mode. Furthermore, we indicate that our approach of directly approximating the gradient is compatible with recent sophisticated stochastic gradient methods (e.g., Adam), and then propose another modal regression method based on neural networks. Finally, the superior performance of the proposed methods is demonstrated on various artificial and benchmark datasets.

Nonlinear ICA Using Auxiliary Variables and Generalized Contrastive Learning

Nonlinear ICA is a fundamental problem for unsupervised representation learning, emphasizing the capacity to recover the underlying latent variables generating the data (i.e., identifiability). Recently, the very first identifiability proofs for nonlinear ICA have been proposed, leveraging the temporal structure of the independent components. Here, we propose a general framework for nonlinear ICA, which, as a special case, can make use of temporal structure. It is based on augmenting the data by an auxiliary variable, such as the time index, the history of the time series, or any other available information. We propose to learn nonlinear ICA by discriminating between true augmented data, or data in which the auxiliary variable has been randomized. This enables the framework to be implemented algorithmically through logistic regression, possibly in a neural network. We provide a comprehensive proof of the identifiability of the model as well as the consistency of our estimation method. The approach not only provides a general theoretical framework combining and generalizing previously proposed nonlinear ICA models and algorithms, but also brings practical advantages.

Neural-Kernelized Conditional Density Estimation

Conditional density estimation is a general framework for solving various problems in machine learning. Among existing methods, non-parametric and/or kernel-based methods are often difficult to use on large datasets, while methods based on neural networks usually make restrictive parametric assumptions on the probability densities. Here, we propose a novel method for estimating the conditional density based on score matching. In contrast to existing methods, we employ scalable neural networks, but do not make explicit parametric assumptions on densities. The key challenge in applying score matching to neural networks is computation of the first- and second-order derivatives of a model for the log-density. We tackle this challenge by developing a new neural-kernelized approach, which can be applied on large datasets with stochastic gradient descent, while the reproducing kernels allow for easy computation of the derivatives needed in score matching. We show that the neural-kernelized function approximator has universal approximation capability and that our method is consistent in conditional density estimation. We numerically demonstrate that our method is useful in high-dimensional conditional density estimation, and compares favourably with existing methods. Finally, we prove that the proposed method has interesting connections to two probabilistically principled frameworks of representation learning: Nonlinear sufficient dimension reduction and nonlinear independent component analysis.

Mode-Seeking Clustering and Density Ridge Estimation via Direct Estimation of Density-Derivative-Ratios

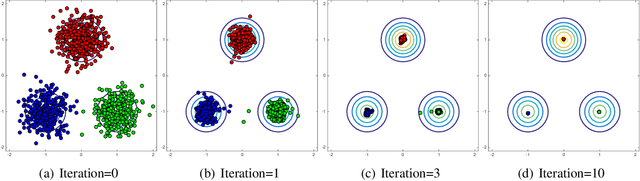
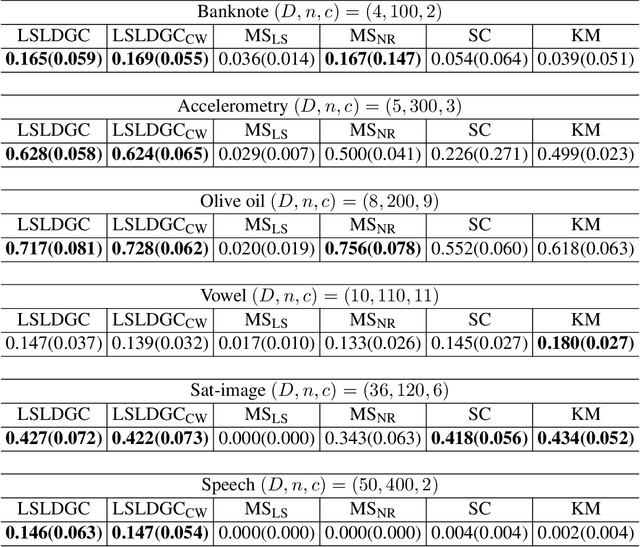
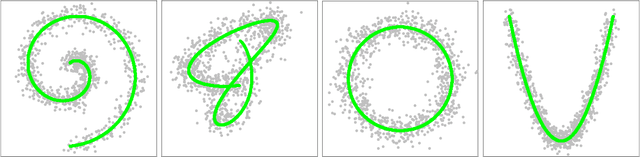
Modes and ridges of the probability density function behind observed data are useful geometric features. Mode-seeking clustering assigns cluster labels by associating data samples with the nearest modes, and estimation of density ridges enables us to find lower-dimensional structures hidden in data. A key technical challenge both in mode-seeking clustering and density ridge estimation is accurate estimation of the ratios of the first- and second-order density derivatives to the density. A naive approach takes a three-step approach of first estimating the data density, then computing its derivatives, and finally taking their ratios. However, this three-step approach can be unreliable because a good density estimator does not necessarily mean a good density derivative estimator, and division by the estimated density could significantly magnify the estimation error. To cope with these problems, we propose a novel estimator for the \emph{density-derivative-ratios}. The proposed estimator does not involve density estimation, but rather \emph{directly} approximates the ratios of density derivatives of any order. Moreover, we establish a convergence rate of the proposed estimator. Based on the proposed estimator, novel methods both for mode-seeking clustering and density ridge estimation are developed, and the respective convergence rates to the mode and ridge of the underlying density are also established. Finally, we experimentally demonstrate that the developed methods significantly outperform existing methods, particularly for relatively high-dimensional data.

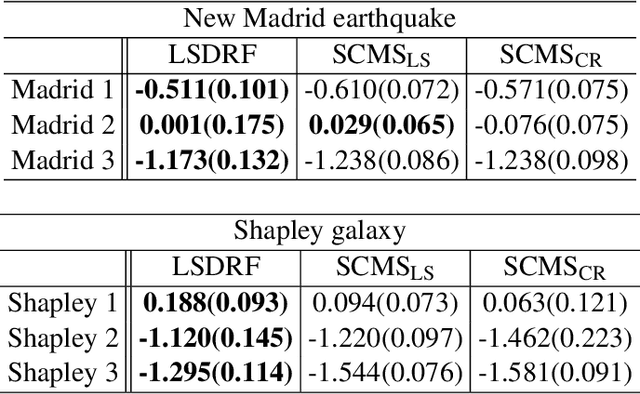
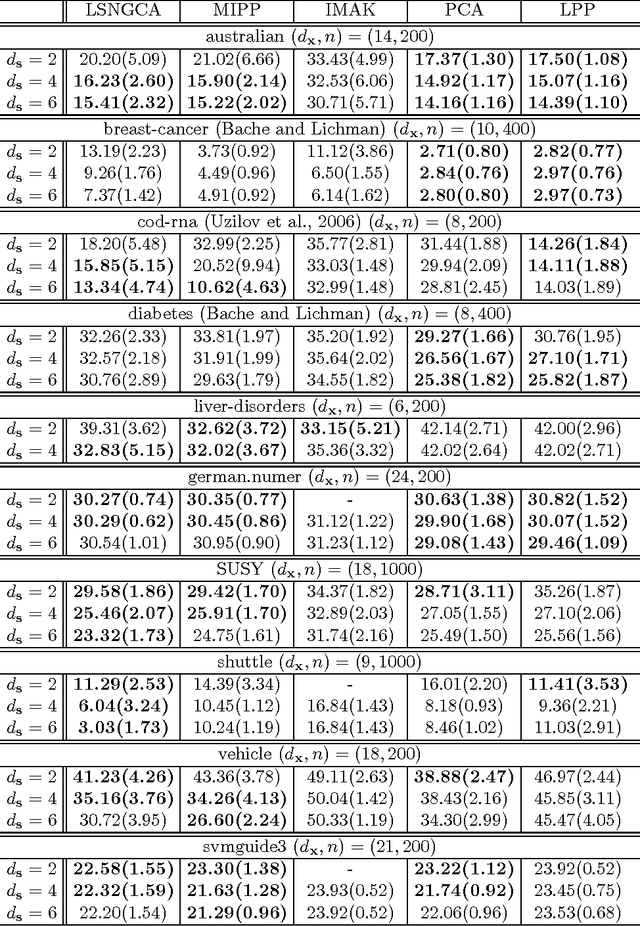
Simultaneous Estimation of Non-Gaussian Components and their Correlation Structure

The statistical dependencies which independent component analysis (ICA) cannot remove often provide rich information beyond the linear independent components. It would thus be very useful to estimate the dependency structure from data. While such models have been proposed, they usually concentrated on higher-order correlations such as energy (square) correlations. Yet, linear correlations are a most fundamental and informative form of dependency in many real data sets. Linear correlations are usually completely removed by ICA and related methods, so they can only be analyzed by developing new methods which explicitly allow for linearly correlated components. In this paper, we propose a probabilistic model of linear non-Gaussian components which are allowed to have both linear and energy correlations. The precision matrix of the linear components is assumed to be randomly generated by a higher-order process and explicitly parametrized by a parameter matrix. The estimation of the parameter matrix is shown to be particularly simple because using score matching, the objective function is a quadratic form. Using simulations with artificial data, we demonstrate that the proposed method improves identifiability of non-Gaussian components by simultaneously learning their correlation structure. Applications on simulated complex cells with natural image input, as well as spectrograms of natural audio data show that the method finds new kinds of dependencies between the components.

Whitening-Free Least-Squares Non-Gaussian Component Analysis

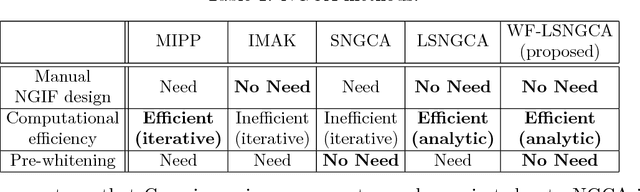
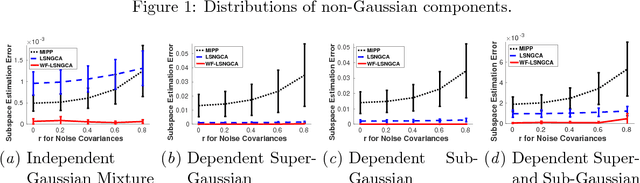
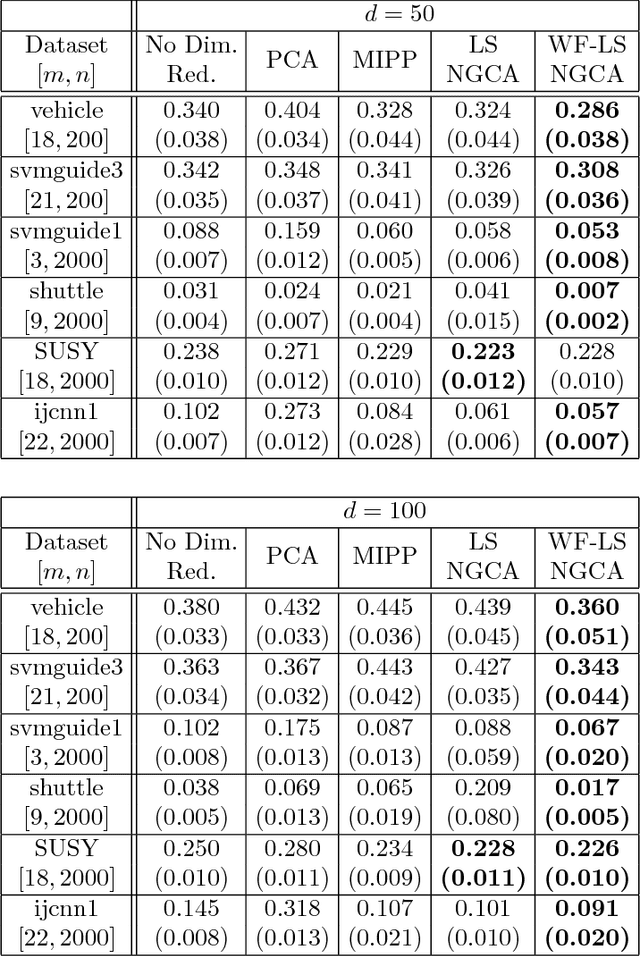
Non-Gaussian component analysis (NGCA) is an unsupervised linear dimension reduction method that extracts low-dimensional non-Gaussian "signals" from high-dimensional data contaminated with Gaussian noise. NGCA can be regarded as a generalization of projection pursuit (PP) and independent component analysis (ICA) to multi-dimensional and dependent non-Gaussian components. Indeed, seminal approaches to NGCA are based on PP and ICA. Recently, a novel NGCA approach called least-squares NGCA (LSNGCA) has been developed, which gives a solution analytically through least-squares estimation of log-density gradients and eigendecomposition. However, since pre-whitening of data is involved in LSNGCA, it performs unreliably when the data covariance matrix is ill-conditioned, which is often the case in high-dimensional data analysis. In this paper, we propose a whitening-free LSNGCA method and experimentally demonstrate its superiority.

Non-Gaussian Component Analysis with Log-Density Gradient Estimation

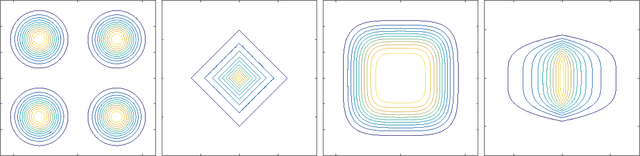
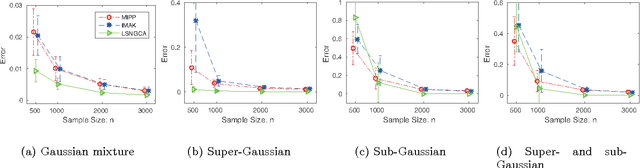
Non-Gaussian component analysis (NGCA) is aimed at identifying a linear subspace such that the projected data follows a non-Gaussian distribution. In this paper, we propose a novel NGCA algorithm based on log-density gradient estimation. Unlike existing methods, the proposed NGCA algorithm identifies the linear subspace by using the eigenvalue decomposition without any iterative procedures, and thus is computationally reasonable. Furthermore, through theoretical analysis, we prove that the identified subspace converges to the true subspace at the optimal parametric rate. Finally, the practical performance of the proposed algorithm is demonstrated on both artificial and benchmark datasets.