Exploration of Unranked Items in Safe Online Learning to Re-Rank

Bandit algorithms for online learning to rank (OLTR) problems often aim to maximize long-term revenue by utilizing user feedback. From a practical point of view, however, such algorithms have a high risk of hurting user experience due to their aggressive exploration. Thus, there has been a rising demand for safe exploration in recent years. One approach to safe exploration is to gradually enhance the quality of an original ranking that is already guaranteed acceptable quality. In this paper, we propose a safe OLTR algorithm that efficiently exchanges one of the items in the current ranking with an item outside the ranking (i.e., an unranked item) to perform exploration. We select an unranked item optimistically to explore based on Kullback-Leibler upper confidence bounds (KL-UCB) and safely re-rank the items including the selected one. Through experiments, we demonstrate that the proposed algorithm improves long-term regret from baselines without any safety violation.

Whitening-Free Least-Squares Non-Gaussian Component Analysis

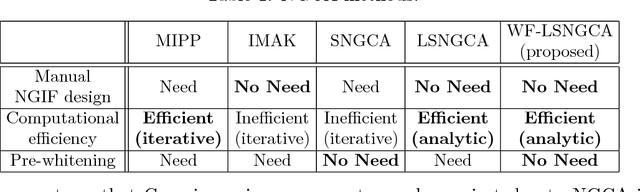
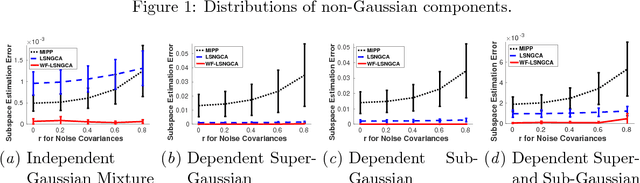
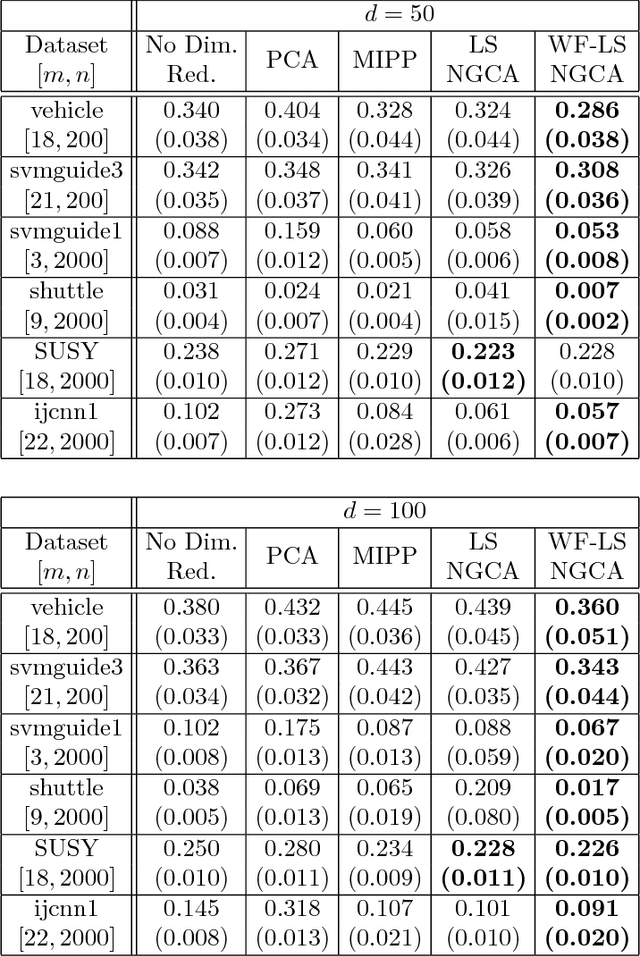
Non-Gaussian component analysis (NGCA) is an unsupervised linear dimension reduction method that extracts low-dimensional non-Gaussian "signals" from high-dimensional data contaminated with Gaussian noise. NGCA can be regarded as a generalization of projection pursuit (PP) and independent component analysis (ICA) to multi-dimensional and dependent non-Gaussian components. Indeed, seminal approaches to NGCA are based on PP and ICA. Recently, a novel NGCA approach called least-squares NGCA (LSNGCA) has been developed, which gives a solution analytically through least-squares estimation of log-density gradients and eigendecomposition. However, since pre-whitening of data is involved in LSNGCA, it performs unreliably when the data covariance matrix is ill-conditioned, which is often the case in high-dimensional data analysis. In this paper, we propose a whitening-free LSNGCA method and experimentally demonstrate its superiority.