Tomoya Sakai
Does medical specialization of VLMs enhance discriminative power?: A comprehensive investigation through feature distribution analysis
Jan 21, 2026Abstract:This study investigates the feature representations produced by publicly available open source medical vision-language models (VLMs). While medical VLMs are expected to capture diagnostically relevant features, their learned representations remain underexplored, and standard evaluations like classification accuracy do not fully reveal if they acquire truly discriminative, lesion-specific features. Understanding these representations is crucial for revealing medical image structures and improving downstream tasks in medical image analysis. This study aims to investigate the feature distributions learned by medical VLMs and evaluate the impact of medical specialization. We analyze the feature distribution of multiple image modalities extracted by some representative medical VLMs across lesion classification datasets on multiple modalities. These distributions were compared them with non-medical VLMs to assess the domain-specific medical training. Our experiments showed that medical VLMs can extract discriminative features that are effective for medical classification tasks. Moreover, it was found that non-medical VLMs with recent improvement with contextual enrichment such as LLM2CLIP produce more refined feature representations. Our results imply that enhancing text encoder is more crucial than training intensively on medical images when developing medical VLMs. Notably, non-medical models are particularly vulnerable to biases introduced by overlaied text strings on images. These findings underscore the need for careful consideration on model selection according to downstream tasks besides potential risks in inference due to background biases such as textual information in images.
TSPulse: Dual Space Tiny Pre-Trained Models for Rapid Time-Series Analysis
May 19, 2025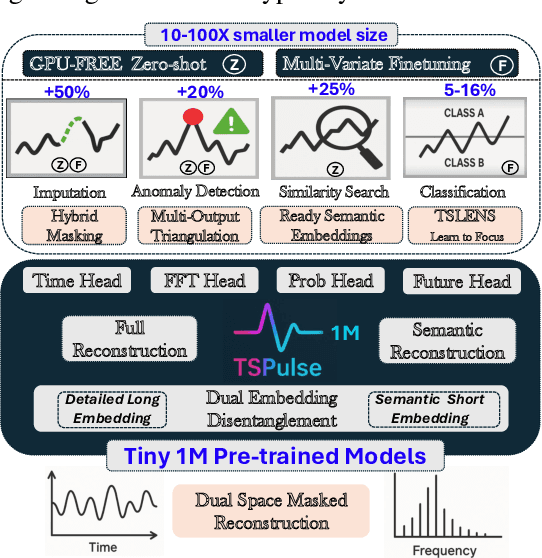

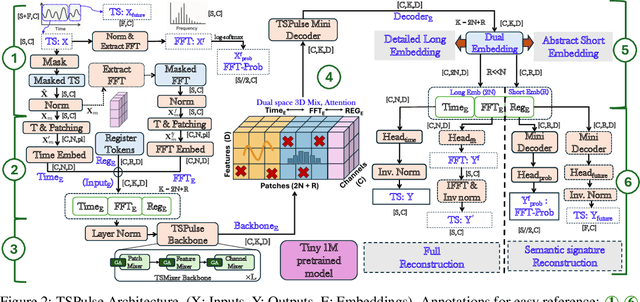

Abstract:The rise of time-series pre-trained models has advanced temporal representation learning, but current state-of-the-art models are often large-scale, requiring substantial compute. We introduce TSPulse, ultra-compact time-series pre-trained models with only 1M parameters, specialized to perform strongly across classification, anomaly detection, imputation, and retrieval tasks. TSPulse introduces innovations at both the architecture and task levels. At the architecture level, it employs a dual-space masked reconstruction, learning from both time and frequency domains to capture complementary signals. This is further enhanced by a dual-embedding disentanglement, generating both detailed embeddings for fine-grained analysis and high-level semantic embeddings for broader task understanding. Notably, TSPulse's semantic embeddings are robust to shifts in time, magnitude, and noise, which is important for robust retrieval. At the task level, TSPulse incorporates TSLens, a fine-tuning component enabling task-specific feature attention. It also introduces a multi-head triangulation technique that correlates deviations from multiple prediction heads, enhancing anomaly detection by fusing complementary model outputs. Additionally, a hybrid mask pretraining is proposed to improves zero-shot imputation by reducing pre-training bias. These architecture and task innovations collectively contribute to TSPulse's significant performance gains: 5-16% on the UEA classification benchmarks, +20% on the TSB-AD anomaly detection leaderboard, +50% in zero-shot imputation, and +25% in time-series retrieval. Remarkably, these results are achieved with just 1M parameters, making TSPulse 10-100X smaller than existing pre-trained models. Its efficiency enables GPU-free inference and rapid pre-training, setting a new standard for efficient time-series pre-trained models. Models will be open-sourced soon.
Unsupervised Deep Learning by Injecting Low-Rank and Sparse Priors
Jun 21, 2021


Abstract:What if deep neural networks can learn from sparsity-inducing priors? When the networks are designed by combining layer modules (CNN, RNN, etc), engineers less exploit the inductive bias, i.e., existing well-known rules or prior knowledge, other than annotated training data sets. We focus on employing sparsity-inducing priors in deep learning to encourage the network to concisely capture the nature of high-dimensional data in an unsupervised way. In order to use non-differentiable sparsity-inducing norms as loss functions, we plug their proximal mappings into the automatic differentiation framework. We demonstrate unsupervised learning of U-Net for background subtraction using low-rank and sparse priors. The U-Net can learn moving objects in a training sequence without any annotation, and successfully detect the foreground objects in test sequences.
Predictive Optimization with Zero-Shot Domain Adaptation
Jan 15, 2021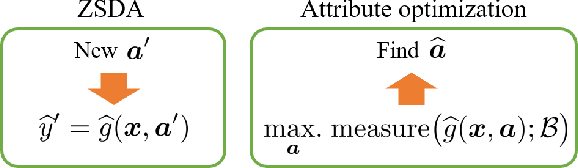
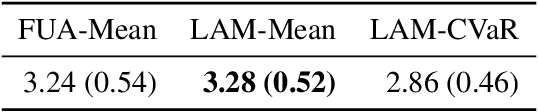
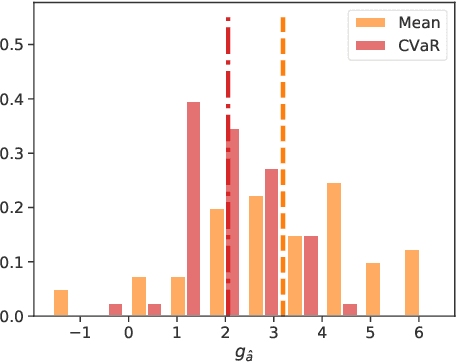

Abstract:Prediction in a new domain without any training sample, called zero-shot domain adaptation (ZSDA), is an important task in domain adaptation. While prediction in a new domain has gained much attention in recent years, in this paper, we investigate another potential of ZSDA. Specifically, instead of predicting responses in a new domain, we find a description of a new domain given a prediction. The task is regarded as predictive optimization, but existing predictive optimization methods have not been extended to handling multiple domains. We propose a simple framework for predictive optimization with ZSDA and analyze the condition in which the optimization problem becomes convex optimization. We also discuss how to handle the interaction of characteristics of a domain in predictive optimization. Through numerical experiments, we demonstrate the potential usefulness of our proposed framework.
Regret Minimization for Causal Inference on Large Treatment Space
Jun 10, 2020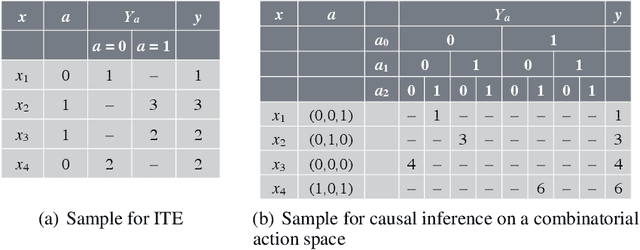
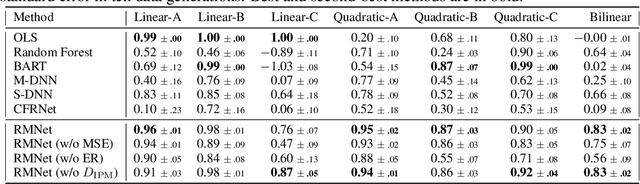
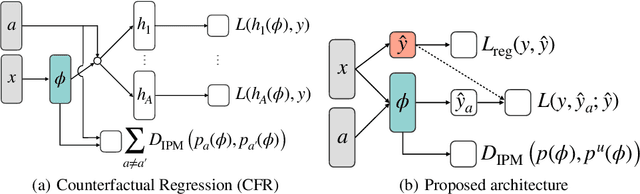
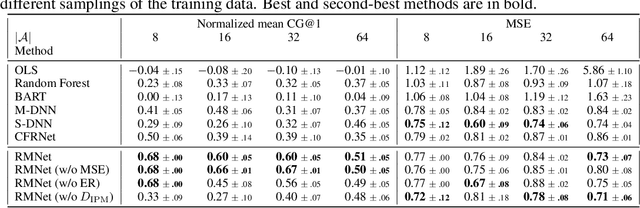
Abstract:Predicting which action (treatment) will lead to a better outcome is a central task in decision support systems. To build a prediction model in real situations, learning from biased observational data is a critical issue due to the lack of randomized controlled trial (RCT) data. To handle such biased observational data, recent efforts in causal inference and counterfactual machine learning have focused on debiased estimation of the potential outcomes on a binary action space and the difference between them, namely, the individual treatment effect. When it comes to a large action space (e.g., selecting an appropriate combination of medicines for a patient), however, the regression accuracy of the potential outcomes is no longer sufficient in practical terms to achieve a good decision-making performance. This is because the mean accuracy on the large action space does not guarantee the nonexistence of a single potential outcome misestimation that might mislead the whole decision. Our proposed loss minimizes a classification error of whether or not the action is relatively good for the individual target among all feasible actions, which further improves the decision-making performance, as we prove. We also propose a network architecture and a regularizer that extracts a debiased representation not only from the individual feature but also from the biased action for better generalization in large action spaces. Extensive experiments on synthetic and semi-synthetic datasets demonstrate the superiority of our method for large combinatorial action spaces.
Do We Need Zero Training Loss After Achieving Zero Training Error?
Feb 20, 2020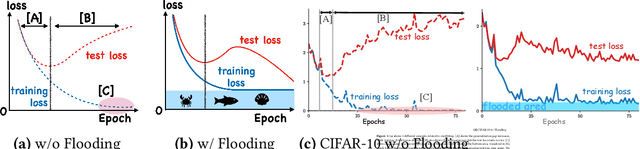
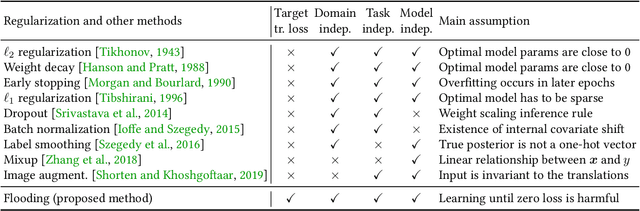
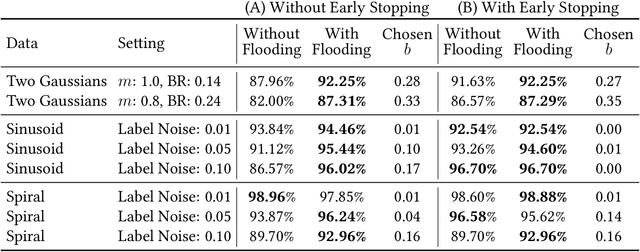
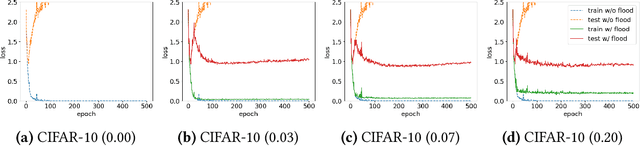
Abstract:Overparameterized deep networks have the capacity to memorize training data with zero training error. Even after memorization, the training loss continues to approach zero, making the model overconfident and the test performance degraded. Since existing regularizers do not directly aim to avoid zero training loss, they often fail to maintain a moderate level of training loss, ending up with a too small or too large loss. We propose a direct solution called flooding that intentionally prevents further reduction of the training loss when it reaches a reasonably small value, which we call the flooding level. Our approach makes the loss float around the flooding level by doing mini-batched gradient descent as usual but gradient ascent if the training loss is below the flooding level. This can be implemented with one line of code, and is compatible with any stochastic optimizer and other regularizers. With flooding, the model will continue to "random walk" with the same non-zero training loss, and we expect it to drift into an area with a flat loss landscape that leads to better generalization. We experimentally show that flooding improves performance and as a byproduct, induces a double descent curve of the test loss.
Robust modal regression with direct log-density derivative estimation
Oct 18, 2019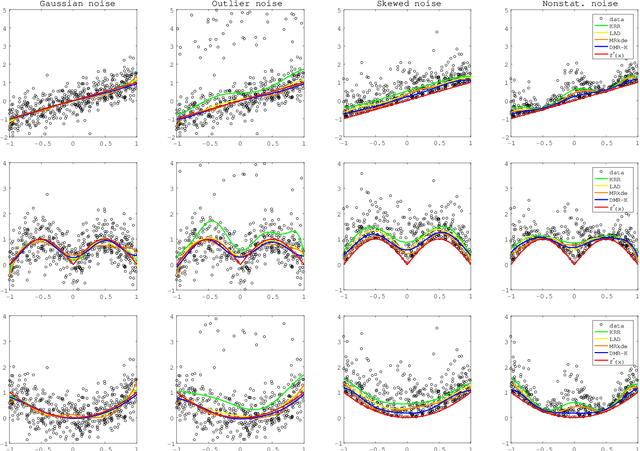
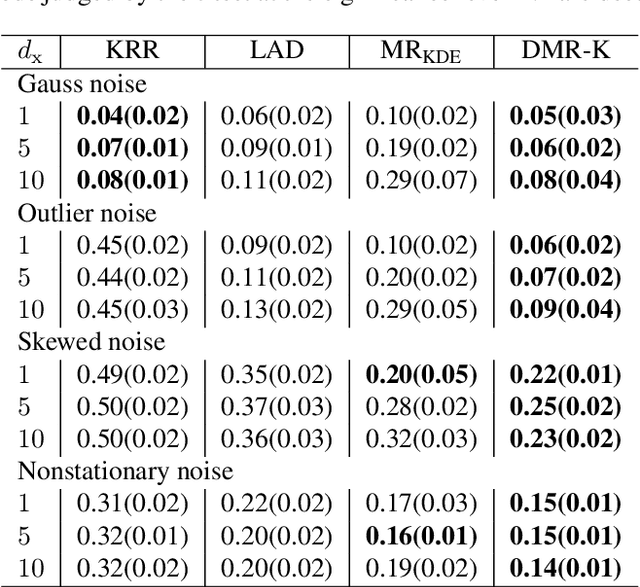
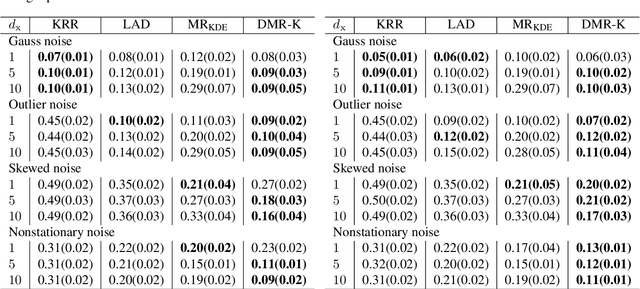
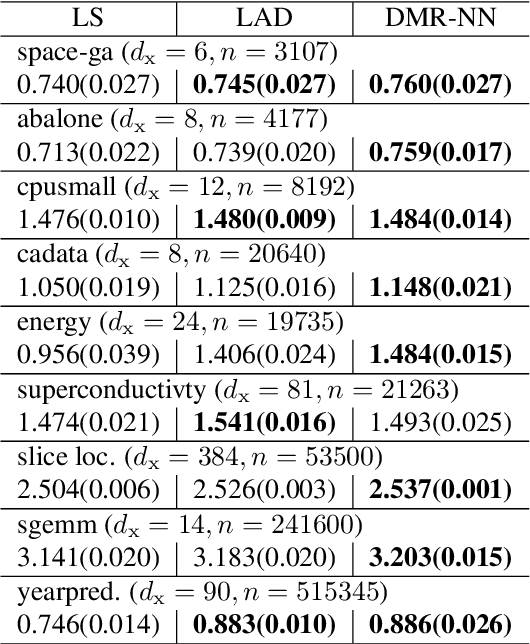
Abstract:Modal regression is aimed at estimating the global mode (i.e., global maximum) of the conditional density function of the output variable given input variables, and has led to regression methods robust against heavy-tailed or skewed noises. The conditional mode is often estimated through maximization of the modal regression risk (MRR). In order to apply a gradient method for the maximization, the fundamental challenge is accurate approximation of the gradient of MRR, not MRR itself. To overcome this challenge, in this paper, we take a novel approach of directly approximating the gradient of MRR. To approximate the gradient, we develop kernelized and neural-network-based versions of the least-squares log-density derivative estimator, which directly approximates the derivative of the log-density without density estimation. With direct approximation of the MRR gradient, we first propose a modal regression method with kernels, and derive a new parameter update rule based on a fixed-point method. Then, the derived update rule is theoretically proved to have a monotonic hill-climbing property towards the conditional mode. Furthermore, we indicate that our approach of directly approximating the gradient is compatible with recent sophisticated stochastic gradient methods (e.g., Adam), and then propose another modal regression method based on neural networks. Finally, the superior performance of the proposed methods is demonstrated on various artificial and benchmark datasets.
Convex Formulation of Multiple Instance Learning from Positive and Unlabeled Bags
May 01, 2018



Abstract:Multiple instance learning (MIL) is a variation of traditional supervised learning problems where data (referred to as bags) are composed of sub-elements (referred to as instances) and only bag labels are available. MIL has a variety of applications such as content-based image retrieval, text categorization and medical diagnosis. Most of the previous work for MIL assume that the training bags are fully labeled. However, it is often difficult to obtain an enough number of labeled bags in practical situations, while many unlabeled bags are available. A learning framework called PU learning (positive and unlabeled learning) can address this problem. In this paper, we propose a convex PU learning method to solve an MIL problem. We experimentally show that the proposed method achieves better performance with significantly lower computational costs than an existing method for PU-MIL.
Binary Matrix Completion Using Unobserved Entries
Mar 13, 2018



Abstract:A matrix completion problem, which aims to recover a complete matrix from its partial observations, is one of the important problems in the machine learning field and has been studied actively. However, there is a discrepancy between the mainstream problem setting, which assumes continuous-valued observations, and some practical applications such as recommendation systems and SNS link predictions where observations take discrete or even binary values. To cope with this problem, Davenport et al. (2014) proposed a binary matrix completion (BMC) problem, where observations are quantized into binary values. Hsieh et al. (2015) proposed a PU (Positive and Unlabeled) matrix completion problem, which is an extension of the BMC problem. This problem targets the setting where we cannot observe negative values, such as SNS link predictions. In the construction of their method for this setting, they introduced a methodology of the classification problem, regarding each matrix entry as a sample. Their risk, which defines losses over unobserved entries as well, indicates the possibility of the use of unobserved entries. In this paper, motivated by a semi-supervised classification method recently proposed by Sakai et al. (2017), we develop a method for the BMC problem which can use all of positive, negative, and unobserved entries, by combining the risks of Davenport et al. (2014) and Hsieh et al. (2015). To the best of our knowledge, this is the first BMC method which exploits all kinds of matrix entries. We experimentally show that an appropriate mixture of risks improves the performance.
Information-Theoretic Representation Learning for Positive-Unlabeled Classification
Feb 12, 2018



Abstract:Recent advances in weakly supervised classification allow us to train a classifier only from positive and unlabeled (PU) data. However, existing PU classification methods typically require an accurate estimate of the class-prior probability, which is a critical bottleneck particularly for high-dimensional data. This problem has been commonly addressed by applying principal component analysis in advance, but such unsupervised dimension reduction can collapse underlying class structure. In this paper, we propose a novel representation learning method from PU data based on the information-maximization principle. Our method does not require class-prior estimation and thus can be used as a preprocessing method for PU classification. Through experiments, we demonstrate that our method combined with deep neural networks highly improves the accuracy of PU class-prior estimation, leading to state-of-the-art PU classification performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge