Semi-Supervised Classification Based on Classification from Positive and Unlabeled Data

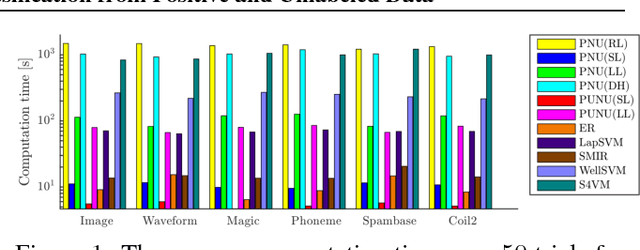
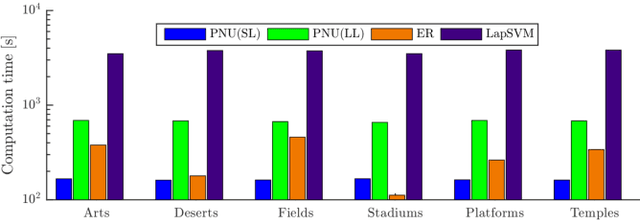
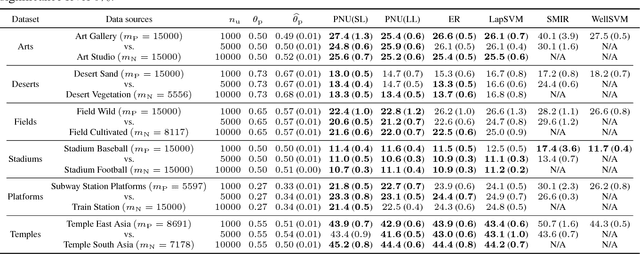
Most of the semi-supervised classification methods developed so far use unlabeled data for regularization purposes under particular distributional assumptions such as the cluster assumption. In contrast, recently developed methods of classification from positive and unlabeled data (PU classification) use unlabeled data for risk evaluation, i.e., label information is directly extracted from unlabeled data. In this paper, we extend PU classification to also incorporate negative data and propose a novel semi-supervised classification approach. We establish generalization error bounds for our novel methods and show that the bounds decrease with respect to the number of unlabeled data without the distributional assumptions that are required in existing semi-supervised classification methods. Through experiments, we demonstrate the usefulness of the proposed methods.

Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning

In PU learning, a binary classifier is trained from positive (P) and unlabeled (U) data without negative (N) data. Although N data is missing, it sometimes outperforms PN learning (i.e., ordinary supervised learning). Hitherto, neither theoretical nor experimental analysis has been given to explain this phenomenon. In this paper, we theoretically compare PU (and NU) learning against PN learning based on the upper bounds on estimation errors. We find simple conditions when PU and NU learning are likely to outperform PN learning, and we prove that, in terms of the upper bounds, either PU or NU learning (depending on the class-prior probability and the sizes of P and N data) given infinite U data will improve on PN learning. Our theoretical findings well agree with the experimental results on artificial and benchmark data even when the experimental setup does not match the theoretical assumptions exactly.

Transductive Learning with Multi-class Volume Approximation

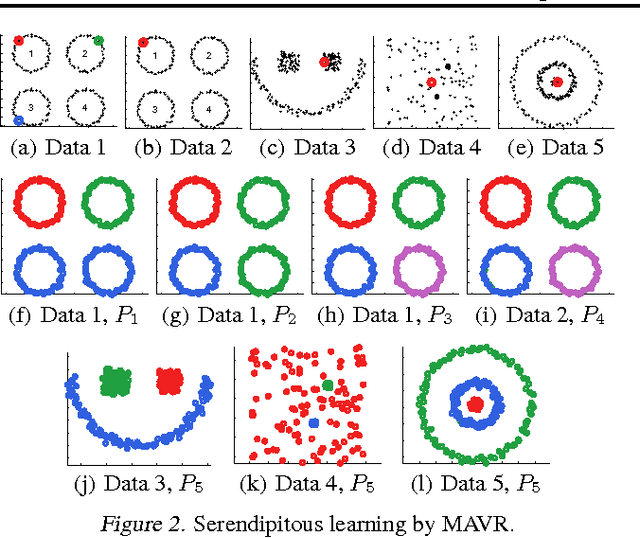
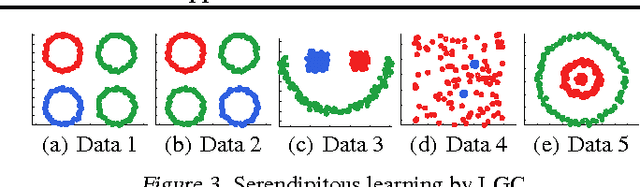
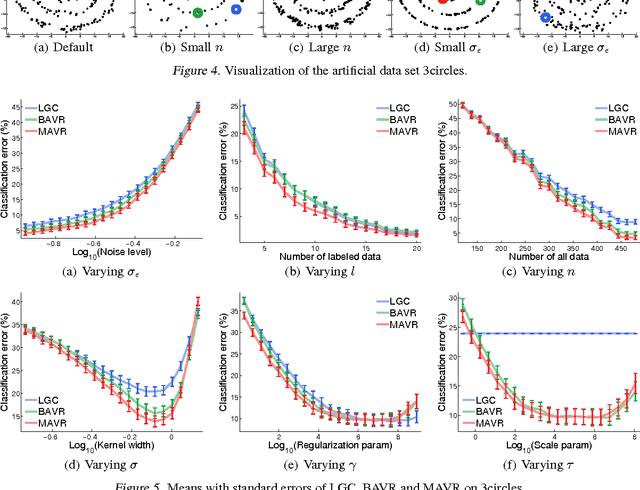
Given a hypothesis space, the large volume principle by Vladimir Vapnik prioritizes equivalence classes according to their volume in the hypothesis space. The volume approximation has hitherto been successfully applied to binary learning problems. In this paper, we extend it naturally to a more general definition which can be applied to several transductive problem settings, such as multi-class, multi-label and serendipitous learning. Even though the resultant learning method involves a non-convex optimization problem, the globally optimal solution is almost surely unique and can be obtained in O(n^3) time. We theoretically provide stability and error analyses for the proposed method, and then experimentally show that it is promising.

Clustering Unclustered Data: Unsupervised Binary Labeling of Two Datasets Having Different Class Balances

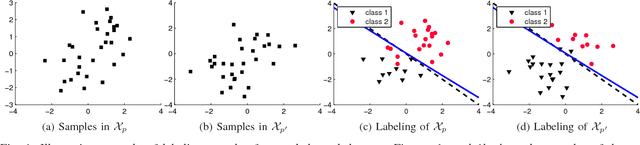
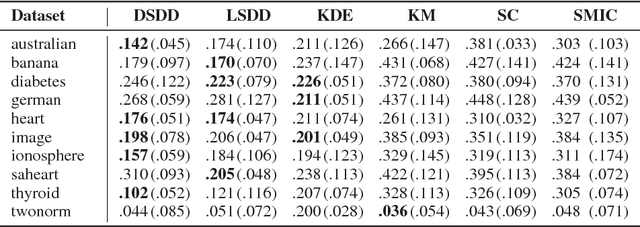
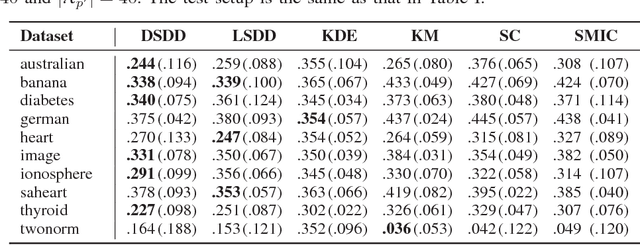
We consider the unsupervised learning problem of assigning labels to unlabeled data. A naive approach is to use clustering methods, but this works well only when data is properly clustered and each cluster corresponds to an underlying class. In this paper, we first show that this unsupervised labeling problem in balanced binary cases can be solved if two unlabeled datasets having different class balances are available. More specifically, estimation of the sign of the difference between probability densities of two unlabeled datasets gives the solution. We then introduce a new method to directly estimate the sign of the density difference without density estimation. Finally, we demonstrate the usefulness of the proposed method against several clustering methods on various toy problems and real-world datasets.

Density-Difference Estimation

We address the problem of estimating the difference between two probability densities. A naive approach is a two-step procedure of first estimating two densities separately and then computing their difference. However, such a two-step procedure does not necessarily work well because the first step is performed without regard to the second step and thus a small error incurred in the first stage can cause a big error in the second stage. In this paper, we propose a single-shot procedure for directly estimating the density difference without separately estimating two densities. We derive a non-parametric finite-sample error bound for the proposed single-shot density-difference estimator and show that it achieves the optimal convergence rate. The usefulness of the proposed method is also demonstrated experimentally.