Transductive Learning with Multi-class Volume Approximation
Paper and Code
Feb 03, 2014
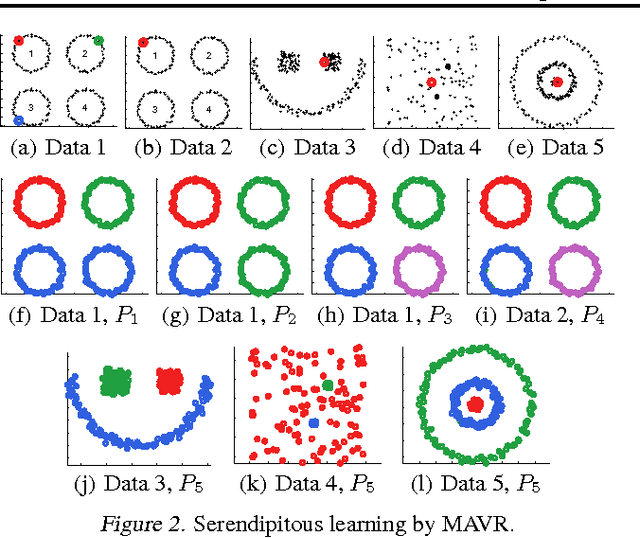
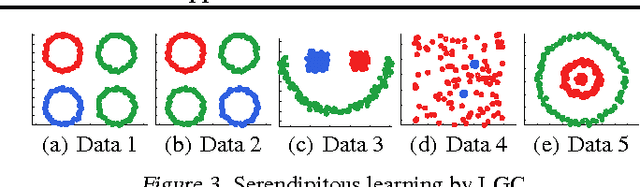
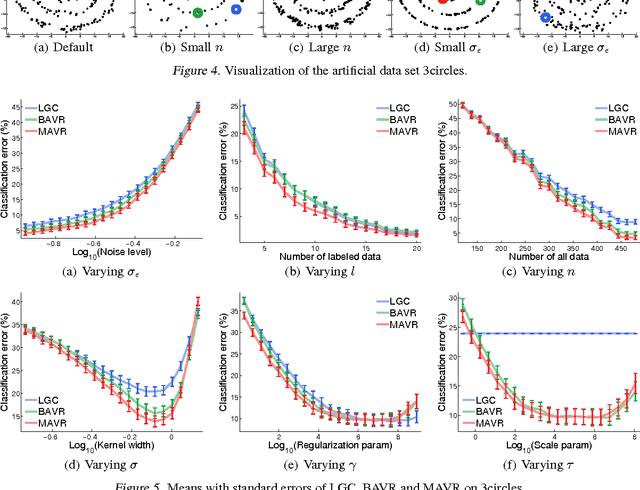
Given a hypothesis space, the large volume principle by Vladimir Vapnik prioritizes equivalence classes according to their volume in the hypothesis space. The volume approximation has hitherto been successfully applied to binary learning problems. In this paper, we extend it naturally to a more general definition which can be applied to several transductive problem settings, such as multi-class, multi-label and serendipitous learning. Even though the resultant learning method involves a non-convex optimization problem, the globally optimal solution is almost surely unique and can be obtained in O(n^3) time. We theoretically provide stability and error analyses for the proposed method, and then experimentally show that it is promising.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge