EDINET-Bench: Evaluating LLMs on Complex Financial Tasks using Japanese Financial Statements

Financial analysis presents complex challenges that could leverage large language model (LLM) capabilities. However, the scarcity of challenging financial datasets, particularly for Japanese financial data, impedes academic innovation in financial analytics. As LLMs advance, this lack of accessible research resources increasingly hinders their development and evaluation in this specialized domain. To address this gap, we introduce EDINET-Bench, an open-source Japanese financial benchmark designed to evaluate the performance of LLMs on challenging financial tasks including accounting fraud detection, earnings forecasting, and industry prediction. EDINET-Bench is constructed by downloading annual reports from the past 10 years from Japan's Electronic Disclosure for Investors' NETwork (EDINET) and automatically assigning labels corresponding to each evaluation task. Our experiments reveal that even state-of-the-art LLMs struggle, performing only slightly better than logistic regression in binary classification for fraud detection and earnings forecasting. These results highlight significant challenges in applying LLMs to real-world financial applications and underscore the need for domain-specific adaptation. Our dataset, benchmark construction code, and evaluation code is publicly available to facilitate future research in finance with LLMs.

Practical estimation of the optimal classification error with soft labels and calibration

While the performance of machine learning systems has experienced significant improvement in recent years, relatively little attention has been paid to the fundamental question: to what extent can we improve our models? This paper provides a means of answering this question in the setting of binary classification, which is practical and theoretically supported. We extend a previous work that utilizes soft labels for estimating the Bayes error, the optimal error rate, in two important ways. First, we theoretically investigate the properties of the bias of the hard-label-based estimator discussed in the original work. We reveal that the decay rate of the bias is adaptive to how well the two class-conditional distributions are separated, and it can decay significantly faster than the previous result suggested as the number of hard labels per instance grows. Second, we tackle a more challenging problem setting: estimation with corrupted soft labels. One might be tempted to use calibrated soft labels instead of clean ones. However, we reveal that calibration guarantee is not enough, that is, even perfectly calibrated soft labels can result in a substantially inaccurate estimate. Then, we show that isotonic calibration can provide a statistically consistent estimator under an assumption weaker than that of the previous work. Our method is instance-free, i.e., we do not assume access to any input instances. This feature allows it to be adopted in practical scenarios where the instances are not available due to privacy issues. Experiments with synthetic and real-world datasets show the validity of our methods and theory.

How Can I Publish My LLM Benchmark Without Giving the True Answers Away?

Publishing a large language model (LLM) benchmark on the Internet risks contaminating future LLMs: the benchmark may be unintentionally (or intentionally) used to train or select a model. A common mitigation is to keep the benchmark private and let participants submit their models or predictions to the organizers. However, this strategy will require trust in a single organization and still permits test-set overfitting through repeated queries. To overcome this issue, we propose a way to publish benchmarks without completely disclosing the ground-truth answers to the questions, while still maintaining the ability to openly evaluate LLMs. Our main idea is to inject randomness to the answers by preparing several logically correct answers, and only include one of them as the solution in the benchmark. This reduces the best possible accuracy, i.e., Bayes accuracy, of the benchmark. Not only is this helpful to keep us from disclosing the ground truth, but this approach also offers a test for detecting data contamination. In principle, even fully capable models should not surpass the Bayes accuracy. If a model surpasses this ceiling despite this expectation, this is a strong signal of data contamination. We present experimental evidence that our method can detect data contamination accurately on a wide range of benchmarks, models, and training methodologies.

Learning with Complementary Labels Revisited: A Consistent Approach via Negative-Unlabeled Learning

Complementary-label learning is a weakly supervised learning problem in which each training example is associated with one or multiple complementary labels indicating the classes to which it does not belong. Existing consistent approaches have relied on the uniform distribution assumption to model the generation of complementary labels, or on an ordinary-label training set to estimate the transition matrix. However, both conditions may not be satisfied in real-world scenarios. In this paper, we propose a novel complementary-label learning approach that does not rely on these conditions. We find that complementary-label learning can be expressed as a set of negative-unlabeled binary classification problems when using the one-versus-rest strategy. This observation allows us to propose a risk-consistent approach with theoretical guarantees. Furthermore, we introduce a risk correction approach to address overfitting problems when using complex models. We also prove the statistical consistency and convergence rate of the corrected risk estimator. Extensive experimental results on both synthetic and real-world benchmark datasets validate the superiority of our proposed approach over state-of-the-art methods.

Flooding Regularization for Stable Training of Generative Adversarial Networks

Generative Adversarial Networks (GANs) have shown remarkable performance in image generation. However, GAN training suffers from the problem of instability. One of the main approaches to address this problem is to modify the loss function, often using regularization terms in addition to changing the type of adversarial losses. This paper focuses on directly regularizing the adversarial loss function. We propose a method that applies flooding, an overfitting suppression method in supervised learning, to GANs to directly prevent the discriminator's loss from becoming excessively low. Flooding requires tuning the flood level, but when applied to GANs, we propose that the appropriate range of flood level settings is determined by the adversarial loss function, supported by theoretical analysis of GANs using the binary cross entropy loss. We experimentally verify that flooding stabilizes GAN training and can be combined with other stabilization techniques. We also reveal that by restricting the discriminator's loss to be no greater than flood level, the training proceeds stably even when the flood level is somewhat high.

Is the Performance of My Deep Network Too Good to Be True? A Direct Approach to Estimating the Bayes Error in Binary Classification

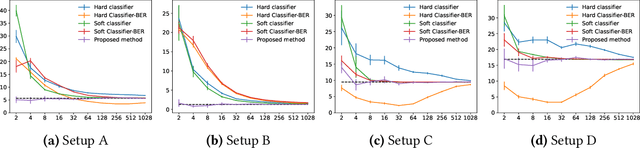
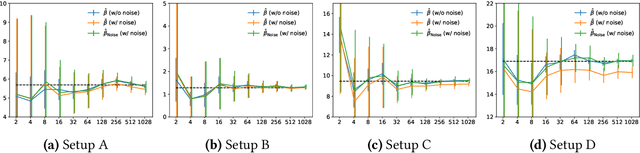
There is a fundamental limitation in the prediction performance that a machine learning model can achieve due to the inevitable uncertainty of the prediction target. In classification problems, this can be characterized by the Bayes error, which is the best achievable error with any classifier. The Bayes error can be used as a criterion to evaluate classifiers with state-of-the-art performance and can be used to detect test set overfitting. We propose a simple and direct Bayes error estimator, where we just take the mean of the labels that show \emph{uncertainty} of the classes. Our flexible approach enables us to perform Bayes error estimation even for weakly supervised data. In contrast to others, our method is model-free and even instance-free. Moreover, it has no hyperparameters and gives a more accurate estimate of the Bayes error than classifier-based baselines. Experiments using our method suggest that a recently proposed classifier, the Vision Transformer, may have already reached the Bayes error for certain benchmark datasets.

LocalDrop: A Hybrid Regularization for Deep Neural Networks

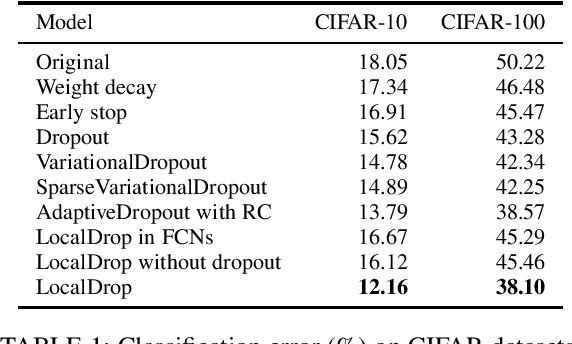
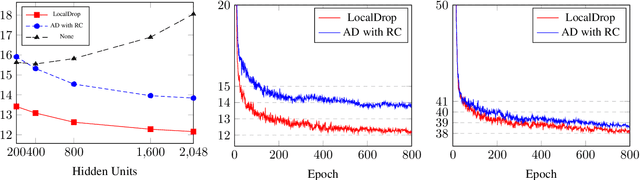
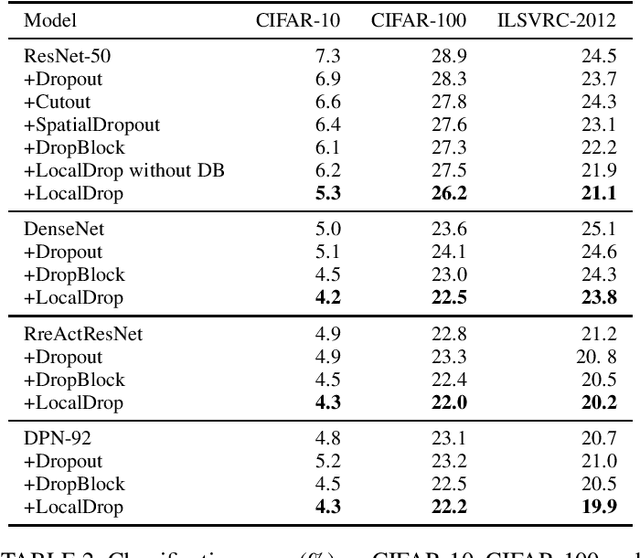
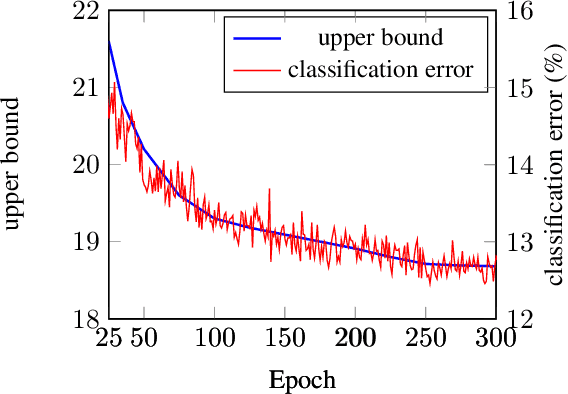
In neural networks, developing regularization algorithms to settle overfitting is one of the major study areas. We propose a new approach for the regularization of neural networks by the local Rademacher complexity called LocalDrop. A new regularization function for both fully-connected networks (FCNs) and convolutional neural networks (CNNs), including drop rates and weight matrices, has been developed based on the proposed upper bound of the local Rademacher complexity by the strict mathematical deduction. The analyses of dropout in FCNs and DropBlock in CNNs with keep rate matrices in different layers are also included in the complexity analyses. With the new regularization function, we establish a two-stage procedure to obtain the optimal keep rate matrix and weight matrix to realize the whole training model. Extensive experiments have been conducted to demonstrate the effectiveness of LocalDrop in different models by comparing it with several algorithms and the effects of different hyperparameters on the final performances.

Do We Need Zero Training Loss After Achieving Zero Training Error?

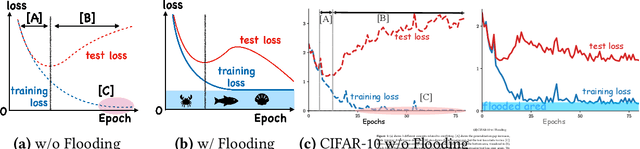
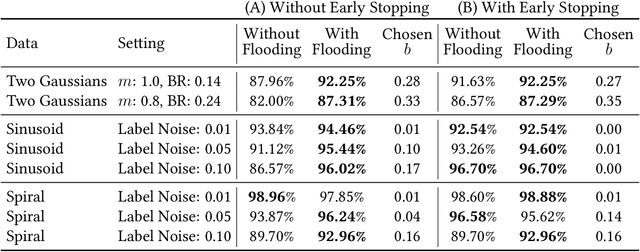
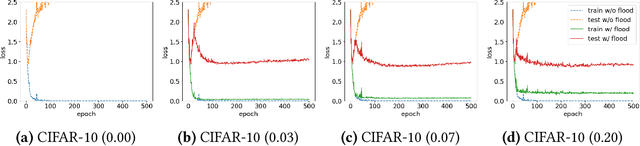
Overparameterized deep networks have the capacity to memorize training data with zero training error. Even after memorization, the training loss continues to approach zero, making the model overconfident and the test performance degraded. Since existing regularizers do not directly aim to avoid zero training loss, they often fail to maintain a moderate level of training loss, ending up with a too small or too large loss. We propose a direct solution called flooding that intentionally prevents further reduction of the training loss when it reaches a reasonably small value, which we call the flooding level. Our approach makes the loss float around the flooding level by doing mini-batched gradient descent as usual but gradient ascent if the training loss is below the flooding level. This can be implemented with one line of code, and is compatible with any stochastic optimizer and other regularizers. With flooding, the model will continue to "random walk" with the same non-zero training loss, and we expect it to drift into an area with a flat loss landscape that leads to better generalization. We experimentally show that flooding improves performance and as a byproduct, induces a double descent curve of the test loss.

Complementary-Label Learning for Arbitrary Losses and Models

In contrast to the standard classification paradigm where the true (or possibly noisy) class is given to each training pattern, complementary-label learning only uses training patterns each equipped with a complementary label. This only specifies one of the classes that the pattern does not belong to. The seminal paper on complementary-label learning proposed an unbiased estimator of the classification risk that can be computed only from complementarily labeled data. However, it required a restrictive condition on the loss functions, making it impossible to use popular losses such as the softmax cross-entropy loss. Recently, another formulation with the softmax cross-entropy loss was proposed with consistency guarantee. However, this formulation does not explicitly involve a risk estimator. Thus model/hyper-parameter selection is not possible by cross-validation---we may need additional ordinarily labeled data for validation purposes, which is not available in the current setup. In this paper, we give a novel general framework of complementary-label learning, and derive an unbiased risk estimator for arbitrary losses and models. We further improve the risk estimator by non-negative correction and demonstrate its superiority through experiments.

Binary Classification from Positive-Confidence Data

Reducing labeling costs in supervised learning is a critical issue in many practical machine learning applications. In this paper, we consider positive-confidence (Pconf) classification, the problem of training a binary classifier only from positive data equipped with confidence. Pconf classification can be regarded as a discriminative extension of one-class classification (which is aimed at "describing" the positive class by clustering-related methods), with ability to tune hyper-parameters for "classifying" positive and negative samples. Pconf classification is also related to positive-unlabeled (PU) classification (which uses hard-labeled positive data and unlabeled data), but the difference is that it enables us to avoid estimating the class priors, which is a critical bottleneck in typical PU classification methods. For the Pconf classification problem, we provide a simple empirical risk minimization framework and give a formulation for linear-in-parameter models that can be implemented easily and computationally efficiently. We also theoretically establish the consistency and estimation error bound for Pconf classification, and demonstrate the practical usefulness of the proposed method for deep neural networks through experiments.