LocalDrop: A Hybrid Regularization for Deep Neural Networks
Paper and Code
Mar 01, 2021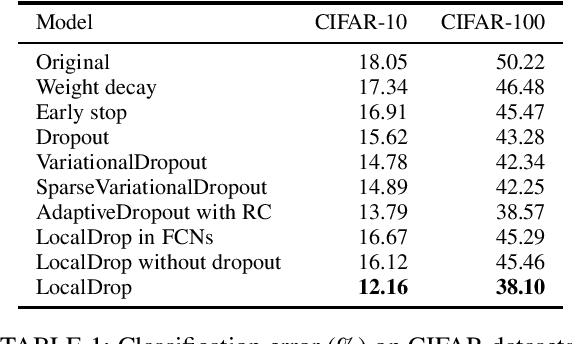
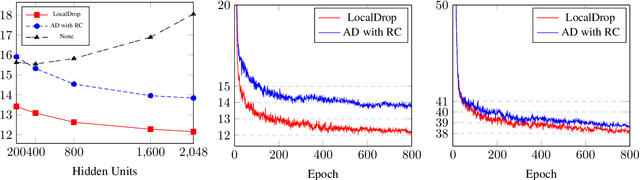
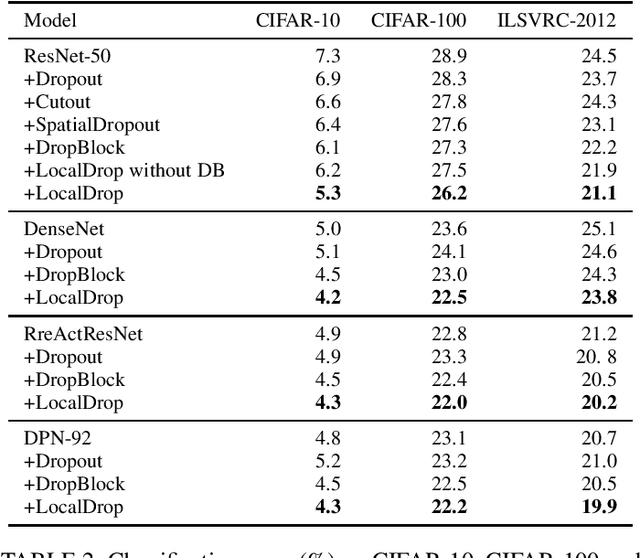
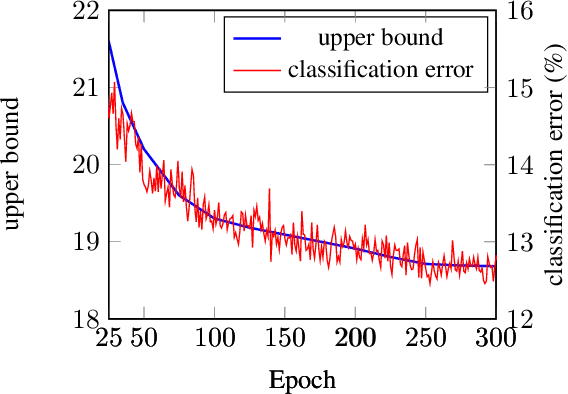
In neural networks, developing regularization algorithms to settle overfitting is one of the major study areas. We propose a new approach for the regularization of neural networks by the local Rademacher complexity called LocalDrop. A new regularization function for both fully-connected networks (FCNs) and convolutional neural networks (CNNs), including drop rates and weight matrices, has been developed based on the proposed upper bound of the local Rademacher complexity by the strict mathematical deduction. The analyses of dropout in FCNs and DropBlock in CNNs with keep rate matrices in different layers are also included in the complexity analyses. With the new regularization function, we establish a two-stage procedure to obtain the optimal keep rate matrix and weight matrix to realize the whole training model. Extensive experiments have been conducted to demonstrate the effectiveness of LocalDrop in different models by comparing it with several algorithms and the effects of different hyperparameters on the final performances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge