Complementary-Label Learning for Arbitrary Losses and Models

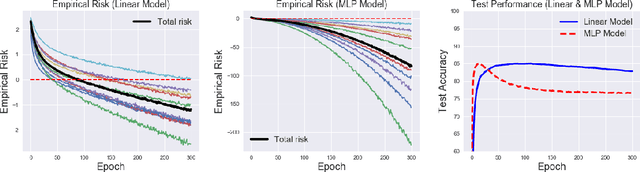
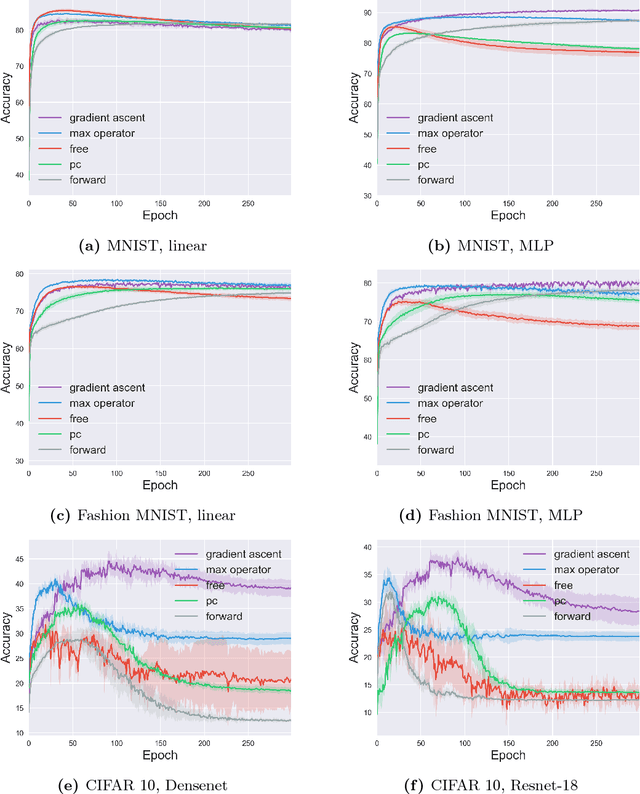
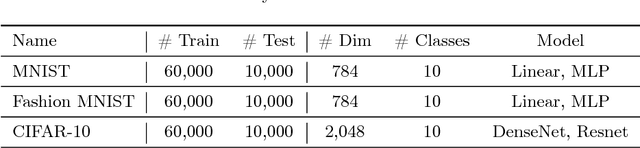
In contrast to the standard classification paradigm where the true (or possibly noisy) class is given to each training pattern, complementary-label learning only uses training patterns each equipped with a complementary label. This only specifies one of the classes that the pattern does not belong to. The seminal paper on complementary-label learning proposed an unbiased estimator of the classification risk that can be computed only from complementarily labeled data. However, it required a restrictive condition on the loss functions, making it impossible to use popular losses such as the softmax cross-entropy loss. Recently, another formulation with the softmax cross-entropy loss was proposed with consistency guarantee. However, this formulation does not explicitly involve a risk estimator. Thus model/hyper-parameter selection is not possible by cross-validation---we may need additional ordinarily labeled data for validation purposes, which is not available in the current setup. In this paper, we give a novel general framework of complementary-label learning, and derive an unbiased risk estimator for arbitrary losses and models. We further improve the risk estimator by non-negative correction and demonstrate its superiority through experiments.