Lower-bounded proper losses for weakly supervised classification

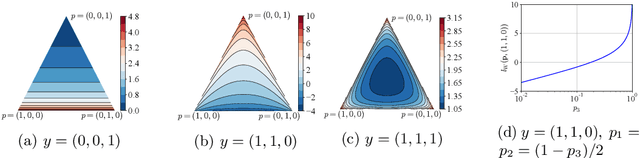
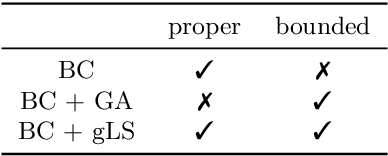
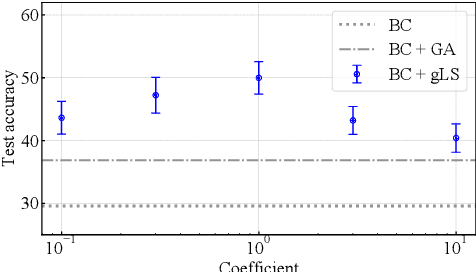
This paper discusses the problem of weakly supervised learning of classification, in which instances are given weak labels that are produced by some label-corruption process. The goal is to derive conditions under which loss functions for weak-label learning are proper and lower-bounded -- two essential requirements for the losses used in class-probability estimation. To this end, we derive a representation theorem for proper losses in supervised learning, which dualizes the Savage representation. We use this theorem to characterize proper weak-label losses and find a condition for them to be lower-bounded. Based on these theoretical findings, we derive a novel regularization scheme called generalized logit squeezing, which makes any proper weak-label loss bounded from below, without losing properness. Furthermore, we experimentally demonstrate the effectiveness of our proposed approach, as compared to improper or unbounded losses. Those results highlight the importance of properness and lower-boundedness. The code is publicly available at https://github.com/yoshum/lower-bounded-proper-losses.

A unified view for unsupervised representation learning with density ratio estimation: Maximization of mutual information, nonlinear ICA and nonlinear subspace estimation

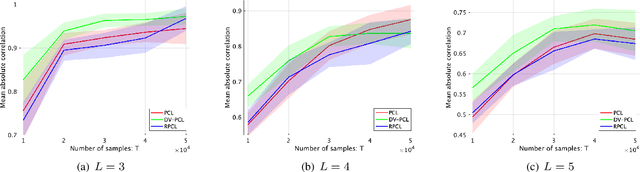
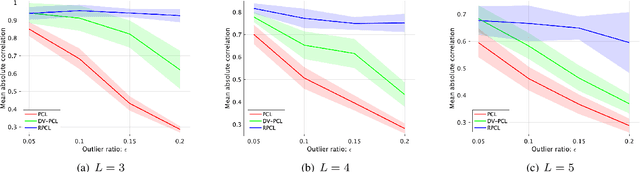
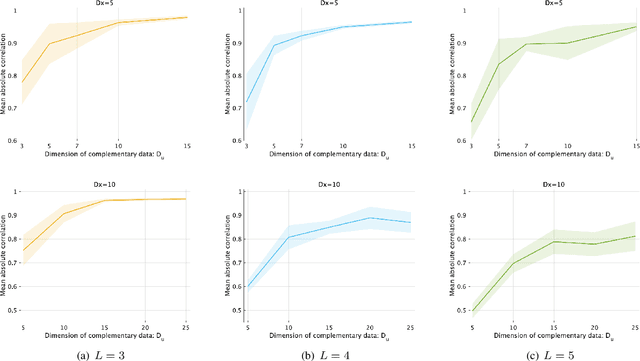
Unsupervised representation learning is one of the most important problems in machine learning. Recent promising methods are based on contrastive learning. However, contrastive learning often relies on heuristic ideas, and therefore it is not easy to understand what contrastive learning is doing. This paper emphasizes that density ratio estimation is a promising goal for unsupervised representation learning, and promotes understanding to contrastive learning. Our primal contribution is to theoretically show that density ratio estimation unifies three frameworks for unsupervised representation learning: Maximization of mutual information (MI), nonlinear independent component analysis (ICA) and a novel framework for estimation of a lower-dimensional nonlinear subspace proposed in this paper. This unified view clarifies under what conditions contrastive learning can be regarded as maximizing MI, performing nonlinear ICA or estimating the lower-dimensional nonlinear subspace in the proposed framework. Furthermore, we also make theoretical contributions in each of the three frameworks: We show that MI can be maximized through density ratio estimation under certain conditions, while our analysis for nonlinear ICA reveals a novel insight for recovery of the latent source components, which is clearly supported by numerical experiments. In addition, some theoretical conditions are also established to estimate a nonlinear subspace in the proposed framework. Based on the unified view, we propose two practical methods for unsupervised representation learning through density ratio estimation: The first method is an outlier-robust method for representation learning, while the second one is a sample-efficient nonlinear ICA method. Finally, we numerically demonstrate usefulness of the proposed methods in nonlinear ICA and through application to a downstream task for classification.

Regret Minimization for Causal Inference on Large Treatment Space

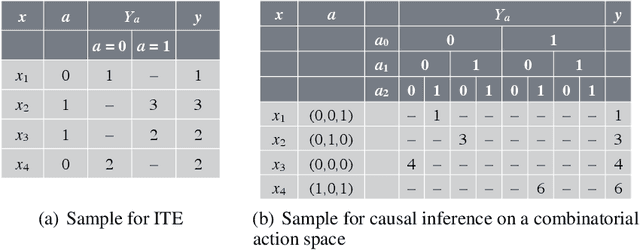
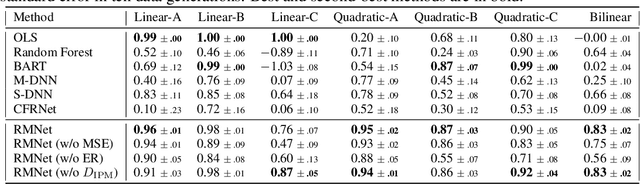
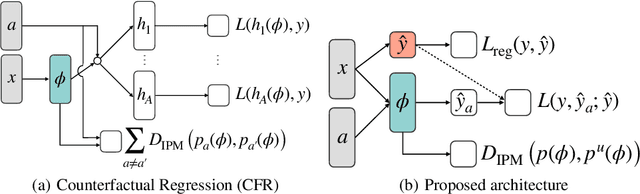
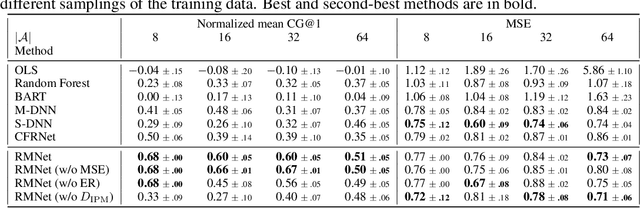
Predicting which action (treatment) will lead to a better outcome is a central task in decision support systems. To build a prediction model in real situations, learning from biased observational data is a critical issue due to the lack of randomized controlled trial (RCT) data. To handle such biased observational data, recent efforts in causal inference and counterfactual machine learning have focused on debiased estimation of the potential outcomes on a binary action space and the difference between them, namely, the individual treatment effect. When it comes to a large action space (e.g., selecting an appropriate combination of medicines for a patient), however, the regression accuracy of the potential outcomes is no longer sufficient in practical terms to achieve a good decision-making performance. This is because the mean accuracy on the large action space does not guarantee the nonexistence of a single potential outcome misestimation that might mislead the whole decision. Our proposed loss minimizes a classification error of whether or not the action is relatively good for the individual target among all feasible actions, which further improves the decision-making performance, as we prove. We also propose a network architecture and a regularizer that extracts a debiased representation not only from the individual feature but also from the biased action for better generalization in large action spaces. Extensive experiments on synthetic and semi-synthetic datasets demonstrate the superiority of our method for large combinatorial action spaces.

Robust contrastive learning and nonlinear ICA in the presence of outliers

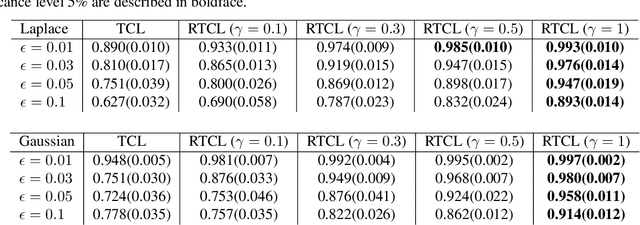
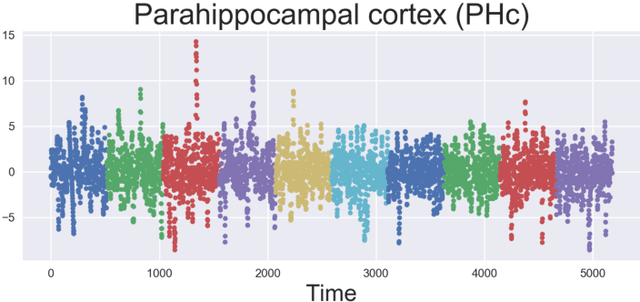
Nonlinear independent component analysis (ICA) is a general framework for unsupervised representation learning, and aimed at recovering the latent variables in data. Recent practical methods perform nonlinear ICA by solving a series of classification problems based on logistic regression. However, it is well-known that logistic regression is vulnerable to outliers, and thus the performance can be strongly weakened by outliers. In this paper, we first theoretically analyze nonlinear ICA models in the presence of outliers. Our analysis implies that estimation in nonlinear ICA can be seriously hampered when outliers exist on the tails of the (noncontaminated) target density, which happens in a typical case of contamination by outliers. We develop two robust nonlinear ICA methods based on the {\gamma}-divergence, which is a robust alternative to the KL-divergence in logistic regression. The proposed methods are shown to have desired robustness properties in the context of nonlinear ICA. We also experimentally demonstrate that the proposed methods are very robust and outperform existing methods in the presence of outliers. Finally, the proposed method is applied to ICA-based causal discovery and shown to find a plausible causal relationship on fMRI data.

Zero-shot Domain Adaptation Based on Attribute Information

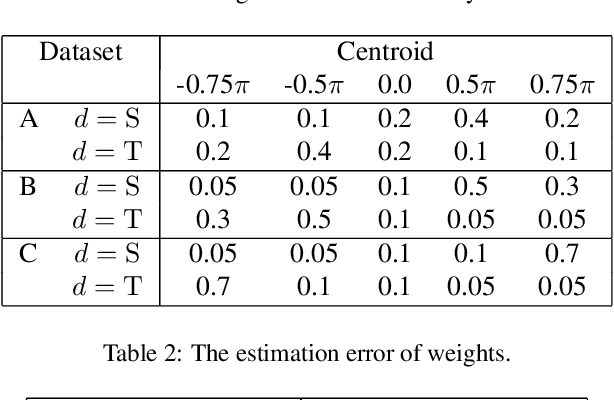
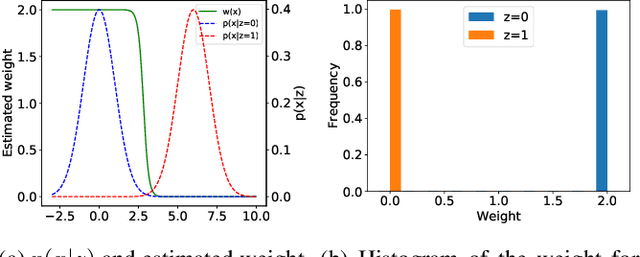
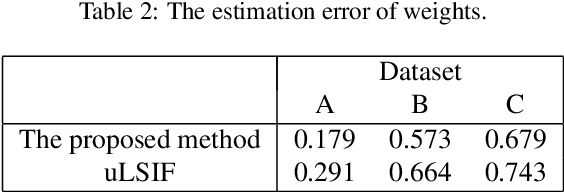
In this paper, we propose a novel domain adaptation method that can be applied without target data. We consider the situation where domain shift is caused by a prior change of a specific factor and assume that we know how the prior changes between source and target domains. We call this factor an attribute, and reformulate the domain adaptation problem to utilize the attribute prior instead of target data. In our method, the source data are reweighted with the sample-wise weight estimated by the attribute prior and the data themselves so that they are useful in the target domain. We theoretically reveal that our method provides more precise estimation of sample-wise transferability than a straightforward attribute-based reweighting approach. Experimental results with both toy datasets and benchmark datasets show that our method can perform well, though it does not use any target data.

Unified estimation framework for unnormalized models with statistical efficiency

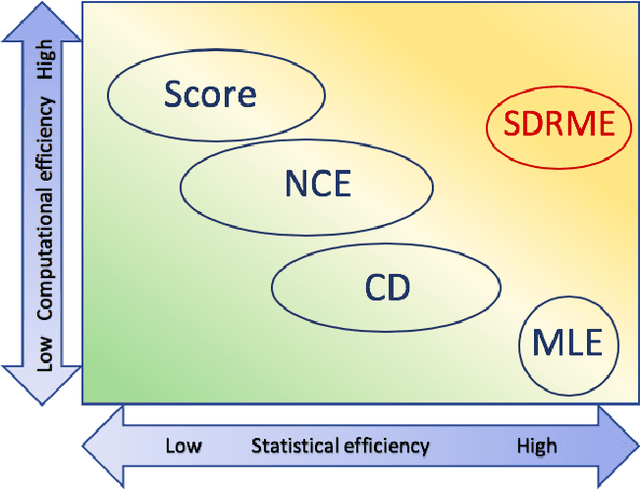
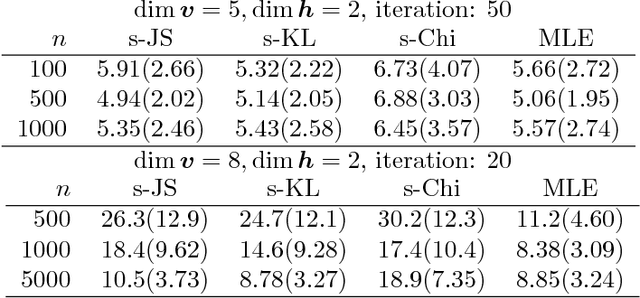
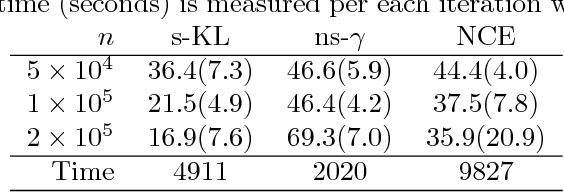
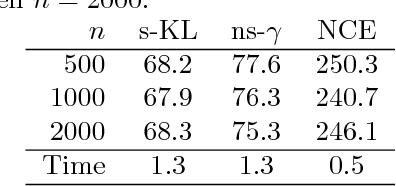
Parameter estimation of unnormalized models is a challenging problem because normalizing constants are not calculated explicitly and maximum likelihood estimation is computationally infeasible. Although some consistent estimators have been proposed earlier, the problem of statistical efficiency does remain. In this study, we propose a unified, statistically efficient estimation framework for unnormalized models and several novel efficient estimators with reasonable computational time regardless of whether the sample space is discrete or continuous. The loss functions of the proposed estimators are derived by combining the following two methods: (1) density-ratio matching using Bregman divergence, and (2) plugging-in nonparametric estimators. We also analyze the properties of the proposed estimators when the unnormalized model is misspecified. Finally, the experimental results demonstrate the advantages of our method over existing approaches.