Identifiability of latent-variable and structural-equation models: from linear to nonlinear

An old problem in multivariate statistics is that linear Gaussian models are often unidentifiable, i.e. some parameters cannot be uniquely estimated. In factor analysis, an orthogonal rotation of the factors is unidentifiable, while in linear regression, the direction of effect cannot be identified. For such linear models, non-Gaussianity of the (latent) variables has been shown to provide identifiability. In the case of factor analysis, this leads to independent component analysis, while in the case of the direction of effect, non-Gaussian versions of structural equation modelling solve the problem. More recently, we have shown how even general nonparametric nonlinear versions of such models can be estimated. Non-Gaussianity is not enough in this case, but assuming we have time series, or that the distributions are suitably modulated by some observed auxiliary variables, the models are identifiable. This paper reviews the identifiability theory for the linear and nonlinear cases, considering both factor analytic models and structural equation models.

Robust contrastive learning and nonlinear ICA in the presence of outliers

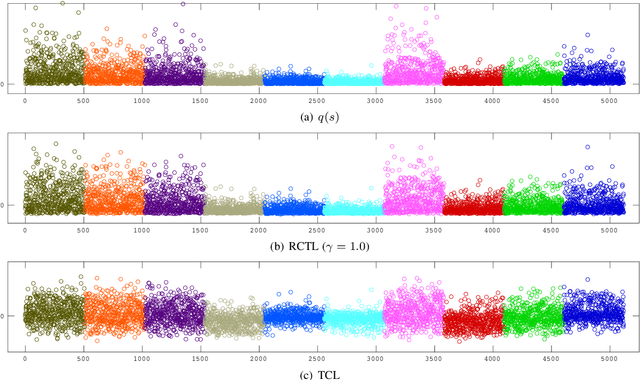
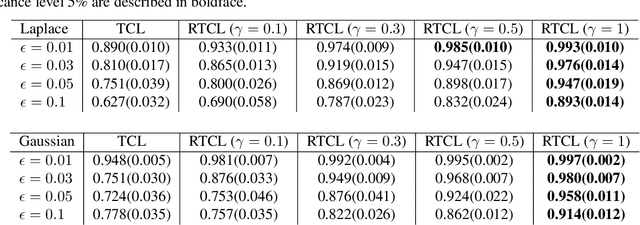
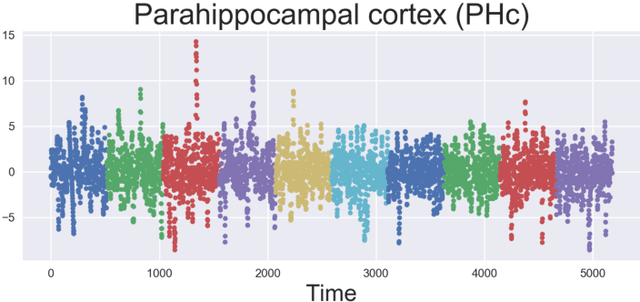
Nonlinear independent component analysis (ICA) is a general framework for unsupervised representation learning, and aimed at recovering the latent variables in data. Recent practical methods perform nonlinear ICA by solving a series of classification problems based on logistic regression. However, it is well-known that logistic regression is vulnerable to outliers, and thus the performance can be strongly weakened by outliers. In this paper, we first theoretically analyze nonlinear ICA models in the presence of outliers. Our analysis implies that estimation in nonlinear ICA can be seriously hampered when outliers exist on the tails of the (noncontaminated) target density, which happens in a typical case of contamination by outliers. We develop two robust nonlinear ICA methods based on the {\gamma}-divergence, which is a robust alternative to the KL-divergence in logistic regression. The proposed methods are shown to have desired robustness properties in the context of nonlinear ICA. We also experimentally demonstrate that the proposed methods are very robust and outperform existing methods in the presence of outliers. Finally, the proposed method is applied to ICA-based causal discovery and shown to find a plausible causal relationship on fMRI data.