Robust Estimation for Kernel Exponential Families with Smoothed Total Variation Distances

In statistical inference, we commonly assume that samples are independent and identically distributed from a probability distribution included in a pre-specified statistical model. However, such an assumption is often violated in practice. Even an unexpected extreme sample called an {\it outlier} can significantly impact classical estimators. Robust statistics studies how to construct reliable statistical methods that efficiently work even when the ideal assumption is violated. Recently, some works revealed that robust estimators such as Tukey's median are well approximated by the generative adversarial net (GAN), a popular learning method for complex generative models using neural networks. GAN is regarded as a learning method using integral probability metrics (IPM), which is a discrepancy measure for probability distributions. In most theoretical analyses of Tukey's median and its GAN-based approximation, however, the Gaussian or elliptical distribution is assumed as the statistical model. In this paper, we explore the application of GAN-like estimators to a general class of statistical models. As the statistical model, we consider the kernel exponential family that includes both finite and infinite-dimensional models. To construct a robust estimator, we propose the smoothed total variation (STV) distance as a class of IPMs. Then, we theoretically investigate the robustness properties of the STV-based estimators. Our analysis reveals that the STV-based estimator is robust against the distribution contamination for the kernel exponential family. Furthermore, we analyze the prediction accuracy of a Monte Carlo approximation method, which circumvents the computational difficulty of the normalization constant.

Stochastic Gradient Descent for Stochastic Doubly-Nonconvex Composite Optimization

The stochastic gradient descent has been widely used for solving composite optimization problems in big data analyses. Many algorithms and convergence properties have been developed. The composite functions were convex primarily and gradually nonconvex composite functions have been adopted to obtain more desirable properties. The convergence properties have been investigated, but only when either of composite functions is nonconvex. There is no convergence property when both composite functions are nonconvex, which is named the \textit{doubly-nonconvex} case.To overcome this difficulty, we assume a simple and weak condition that the penalty function is \textit{quasiconvex} and then we obtain convergence properties for the stochastic doubly-nonconvex composite optimization problem.The convergence rate obtained here is of the same order as the existing work.We deeply analyze the convergence rate with the constant step size and mini-batch size and give the optimal convergence rate with appropriate sizes, which is superior to the existing work. Experimental results illustrate that our method is superior to existing methods.

Robust and Sparse Regression in GLM by Stochastic Optimization

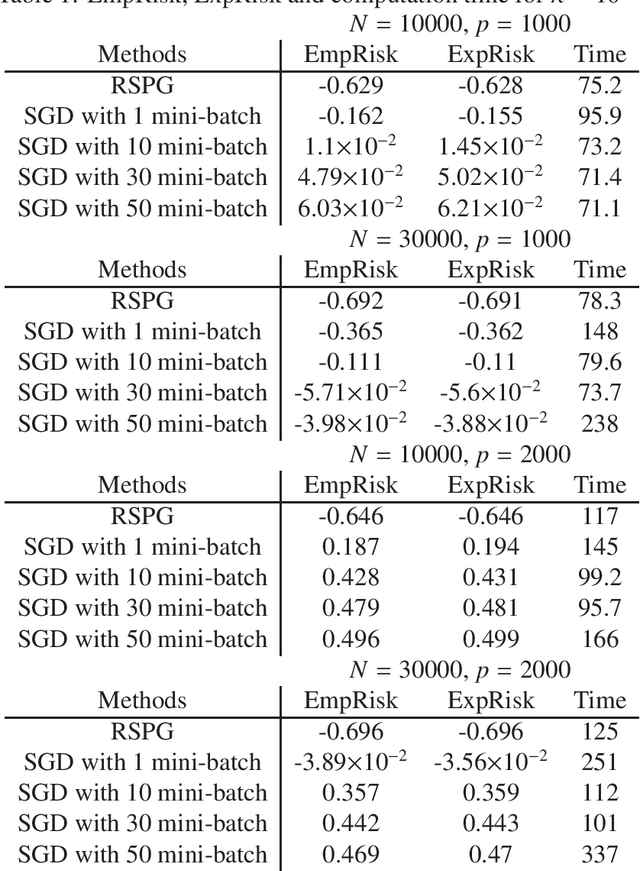
The generalized linear model (GLM) plays a key role in regression analyses. In high-dimensional data, the sparse GLM has been used but it is not robust against outliers. Recently, the robust methods have been proposed for the specific example of the sparse GLM. Among them, we focus on the robust and sparse linear regression based on the $\gamma$-divergence. The estimator of the $\gamma$-divergence has strong robustness under heavy contamination. In this paper, we extend the robust and sparse linear regression based on the $\gamma$-divergence to the robust and sparse GLM based on the $\gamma$-divergence with a stochastic optimization approach in order to obtain the estimate. We adopt the randomized stochastic projected gradient descent as a stochastic optimization approach and extend the established convergence property to the classical first-order necessary condition. By virtue of the stochastic optimization approach, we can efficiently estimate parameters for very large problems. Particularly, we show the linear regression, logistic regression and Poisson regression with $L_1$ regularization in detail as specific examples of robust and sparse GLM. In numerical experiments and real data analysis, the proposed method outperformed comparative methods.

Robust and Sparse Regression via $γ$-divergence

In high-dimensional data, many sparse regression methods have been proposed. However, they may not be robust against outliers. Recently, the use of density power weight has been studied for robust parameter estimation and the corresponding divergences have been discussed. One of such divergences is the $\gamma$-divergence and the robust estimator using the $\gamma$-divergence is known for having a strong robustness. In this paper, we consider the robust and sparse regression based on $\gamma$-divergence. We extend the $\gamma$-divergence to the regression problem and show that it has a strong robustness under heavy contamination even when outliers are heterogeneous. The loss function is constructed by an empirical estimate of the $\gamma$-divergence with sparse regularization and the parameter estimate is defined as the minimizer of the loss function. To obtain the robust and sparse estimate, we propose an efficient update algorithm which has a monotone decreasing property of the loss function. Particularly, we discuss a linear regression problem with $L_1$ regularization in detail. In numerical experiments and real data analyses, we see that the proposed method outperforms past robust and sparse methods.