Surrogate Graph Partitioning for Spatial Prediction

Spatial prediction refers to the estimation of unobserved values from spatially distributed observations. Although recent advances have improved the capacity to model diverse observation types, adoption in practice remains limited in industries that demand interpretability. To mitigate this gap, surrogate models that explain black-box predictors provide a promising path toward interpretable decision making. In this study, we propose a graph partitioning problem to construct spatial segments that minimize the sum of within-segment variances of individual predictions. The assignment of data points to segments can be formulated as a mixed-integer quadratic programming problem. While this formulation potentially enables the identification of exact segments, its computational complexity becomes prohibitive as the number of data points increases. Motivated by this challenge, we develop an approximation scheme that leverages the structural properties of graph partitioning. Experimental results demonstrate the computational efficiency of this approximation in identifying spatial segments.

Learning Survival Models with Right-Censored Reporting Delays

Survival analysis is a statistical technique used to estimate the time until an event occurs. Although it is applied across a wide range of fields, adjusting for reporting delays under practical constraints remains a significant challenge in the insurance industry. Such delays render event occurrences unobservable when their reports are subject to right censoring. This issue becomes particularly critical when estimating hazard rates for newly enrolled cohorts with limited follow-up due to administrative censoring. Our study addresses this challenge by jointly modeling the parametric hazard functions of event occurrences and report timings. The joint probability distribution is marginalized over the latent event occurrence status. We construct an estimator for the proposed survival model and establish its asymptotic consistency. Furthermore, we develop an expectation-maximization algorithm to compute its estimates. Using these findings, we propose a two-stage estimation procedure based on a parametric proportional hazards model to evaluate observations subject to administrative censoring. Experimental results demonstrate that our method effectively improves the timeliness of risk evaluation for newly enrolled cohorts.

Sparse Linear Regression when Noises and Covariates are Heavy-Tailed and Contaminated by Outliers

We investigate a problem estimating coefficients of linear regression under sparsity assumption when covariates and noises are sampled from heavy tailed distributions. Additionally, we consider the situation where not only covariates and noises are sampled from heavy tailed distributions but also contaminated by outliers. Our estimators can be computed efficiently, and exhibit sharp error bounds.

Adaptive Lasso, Transfer Lasso, and Beyond: An Asymptotic Perspective

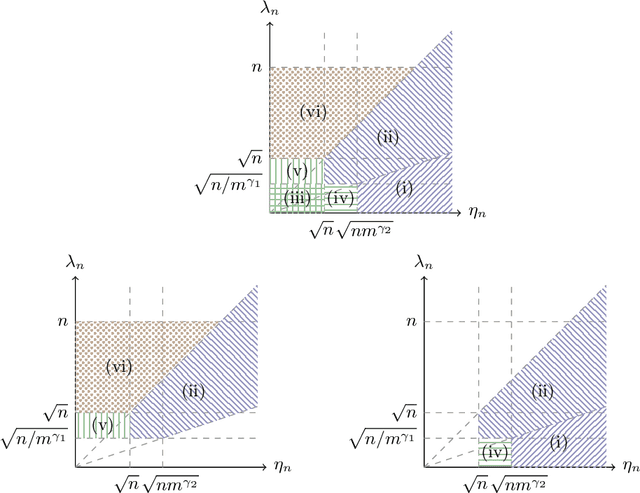
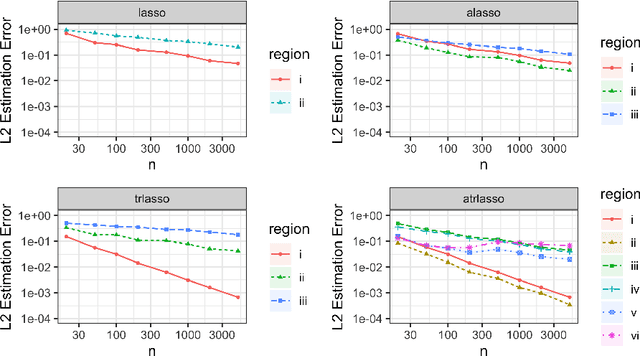
This paper presents a comprehensive exploration of the theoretical properties inherent in the Adaptive Lasso and the Transfer Lasso. The Adaptive Lasso, a well-established method, employs regularization divided by initial estimators and is characterized by asymptotic normality and variable selection consistency. In contrast, the recently proposed Transfer Lasso employs regularization subtracted by initial estimators with the demonstrated capacity to curtail non-asymptotic estimation errors. A pivotal question thus emerges: Given the distinct ways the Adaptive Lasso and the Transfer Lasso employ initial estimators, what benefits or drawbacks does this disparity confer upon each method? This paper conducts a theoretical examination of the asymptotic properties of the Transfer Lasso, thereby elucidating its differentiation from the Adaptive Lasso. Informed by the findings of this analysis, we introduce a novel method, one that amalgamates the strengths and compensates for the weaknesses of both methods. The paper concludes with validations of our theory and comparisons of the methods via simulation experiments.

Outlier Robust and Sparse Estimation of Linear Regression Coefficients

We consider outlier robust and sparse estimation of linear regression coefficients when covariates and noise are sampled, respectively, from an $\mathfrak{L}$-subGaussian distribution and a heavy-tailed distribution, and additionally, the covariates and noise are contaminated by adversarial outliers. We deal with two cases: known or unknown covariance of the covariates. Particularly, in the former case, our estimator attains nearly information theoretical optimal error bound, and our error bound is sharper than that of earlier studies dealing with similar situations. Our estimator analysis relies heavily on Generic Chaining to derive sharp error bounds.

Adversarial robust weighted Huber regression

We propose a novel method to estimate the coefficients of linear regression when outputs and inputs are contaminated by malicious outliers. Our method consists of two-step: (i) Make appropriate weights $\left\{\hat{w}_i\right\}_{i=1}^n$ such that the weighted sample mean of regression covariates robustly estimates the population mean of the regression covariate, (ii) Process Huber regression using $\left\{\hat{w}_i\right\}_{i=1}^n$. When (a) the regression covariate is a sequence with i.i.d. random vectors drawn from sub-Gaussian distribution with unknown mean and known identity covariance and (b) the absolute moment of the random noise is finite, our method attains a faster convergence rate than Diakonikolas, Kong and Stewart (2019) and Cherapanamjeri et al. (2020). Furthermore, our result is minimax optimal up to constant factor. When (a) the regression covariate is a sequence with i.i.d. random vectors drawn from heavy tailed distribution with unknown mean and bounded kurtosis and (b) the absolute moment of the random noise is finite, our method attains a convergence rate, which is minimax optimal up to constant factor.

Adversarial Robust Low Rank Matrix Estimation: Compressed Sensing and Matrix Completion

We consider robust low rank matrix estimation when random noise is heavy-tailed and output is contaminated by adversarial noise. Under the clear conditions, we firstly attain a fast convergence rate for low rank matrix estimation including compressed sensing and matrix completion with convex estimators.

Estimation of Structural Causal Model via Sparsely Mixing Independent Component Analysis

We consider the problem of inferring the causal structure from observational data, especially when the structure is sparse. This type of problem is usually formulated as an inference of a directed acyclic graph (DAG) model. The linear non-Gaussian acyclic model (LiNGAM) is one of the most successful DAG models, and various estimation methods have been developed. However, existing methods are not efficient for some reasons: (i) the sparse structure is not always incorporated in causal order estimation, and (ii) the whole information of the data is not used in parameter estimation. To address {these issues}, we propose a new estimation method for a linear DAG model with non-Gaussian noises. The proposed method is based on the log-likelihood of independent component analysis (ICA) with two penalty terms related to the sparsity and the consistency condition. The proposed method enables us to estimate the causal order and the parameters simultaneously. For stable and efficient optimization, we propose some devices, such as a modified natural gradient. Numerical experiments show that the proposed method outperforms existing methods, including LiNGAM and NOTEARS.

Transfer Learning via $\ell_1$ Regularization

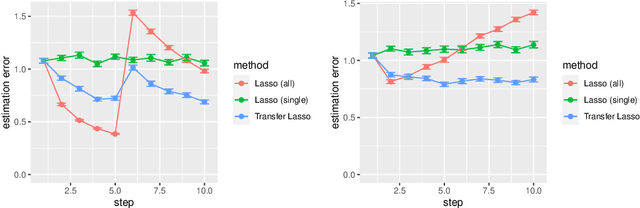
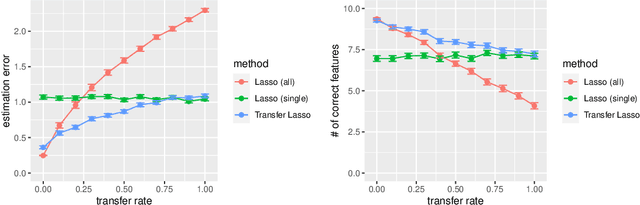
Machine learning algorithms typically require abundant data under a stationary environment. However, environments are nonstationary in many real-world applications. Critical issues lie in how to effectively adapt models under an ever-changing environment. We propose a method for transferring knowledge from a source domain to a target domain via $\ell_1$ regularization. We incorporate $\ell_1$ regularization of differences between source parameters and target parameters, in addition to an ordinary $\ell_1$ regularization. Hence, our method yields sparsity for both the estimates themselves and changes of the estimates. The proposed method has a tight estimation error bound under a stationary environment, and the estimate remains unchanged from the source estimate under small residuals. Moreover, the estimate is consistent with the underlying function, even when the source estimate is mistaken due to nonstationarity. Empirical results demonstrate that the proposed method effectively balances stability and plasticity.

Robust estimation with Lasso when outputs are adversarially contaminated

We consider robust estimation when outputs are adversarially contaminated. Nguyen and Tran (2012) proposed an extended Lasso for robust parameter estimation and then they showed the convergence rate of the estimation error. Recently, Dalalyan and Thompson (2019) gave some useful inequalities and then they showed a sharper convergence rate than Nguyen and Tran (2012) . They focused on the fact that the minimization problem of the extended Lasso can become that of the penalized Huber loss function with $L_1$ penalty. The distinguishing point is that the Huber loss function includes an extra tuning parameter, which is different from the conventional method. However, there is a critical mistake in the proof of Dalalyan and Thompson (2019). We improve the proof and then we give a sharper convergence rate than Nguyen and Tran (2012) , when the number of outliers is larger. The significance of our proof is to use some specific properties of the Huber function. Such techniques have not been used in the past proofs.