Adaptive Lasso, Transfer Lasso, and Beyond: An Asymptotic Perspective

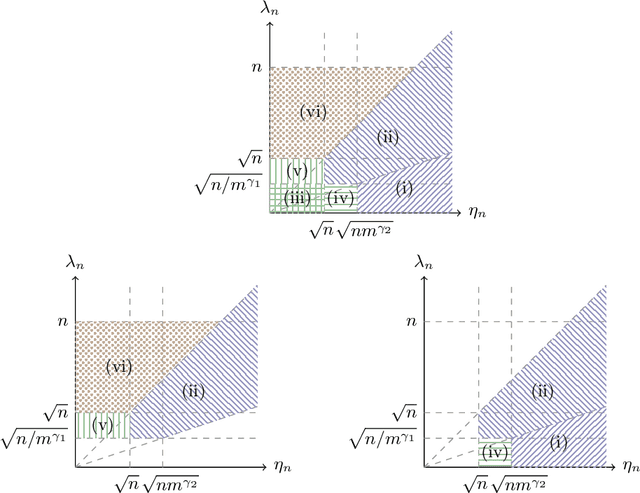
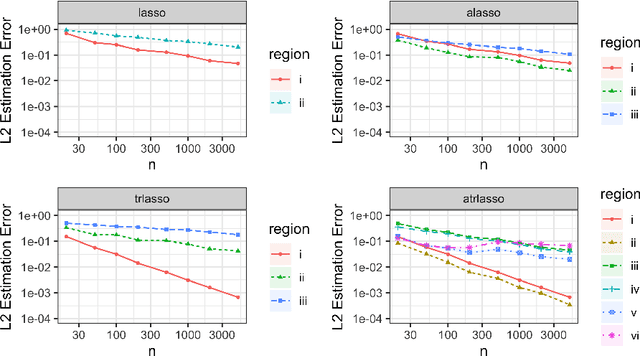
This paper presents a comprehensive exploration of the theoretical properties inherent in the Adaptive Lasso and the Transfer Lasso. The Adaptive Lasso, a well-established method, employs regularization divided by initial estimators and is characterized by asymptotic normality and variable selection consistency. In contrast, the recently proposed Transfer Lasso employs regularization subtracted by initial estimators with the demonstrated capacity to curtail non-asymptotic estimation errors. A pivotal question thus emerges: Given the distinct ways the Adaptive Lasso and the Transfer Lasso employ initial estimators, what benefits or drawbacks does this disparity confer upon each method? This paper conducts a theoretical examination of the asymptotic properties of the Transfer Lasso, thereby elucidating its differentiation from the Adaptive Lasso. Informed by the findings of this analysis, we introduce a novel method, one that amalgamates the strengths and compensates for the weaknesses of both methods. The paper concludes with validations of our theory and comparisons of the methods via simulation experiments.

Transfer Learning via $\ell_1$ Regularization

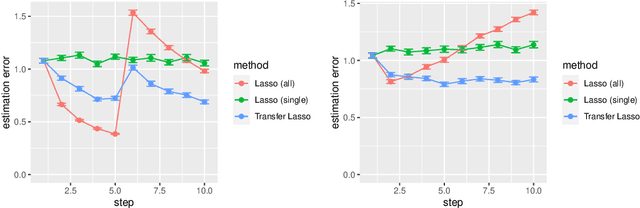
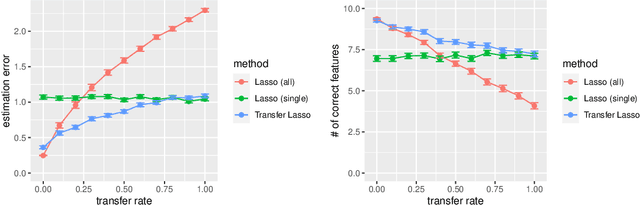
Machine learning algorithms typically require abundant data under a stationary environment. However, environments are nonstationary in many real-world applications. Critical issues lie in how to effectively adapt models under an ever-changing environment. We propose a method for transferring knowledge from a source domain to a target domain via $\ell_1$ regularization. We incorporate $\ell_1$ regularization of differences between source parameters and target parameters, in addition to an ordinary $\ell_1$ regularization. Hence, our method yields sparsity for both the estimates themselves and changes of the estimates. The proposed method has a tight estimation error bound under a stationary environment, and the estimate remains unchanged from the source estimate under small residuals. Moreover, the estimate is consistent with the underlying function, even when the source estimate is mistaken due to nonstationarity. Empirical results demonstrate that the proposed method effectively balances stability and plasticity.

HMLasso: Lasso for High Dimensional and Highly Missing Data

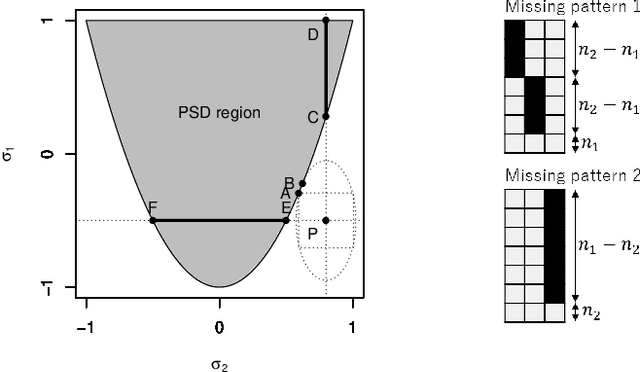
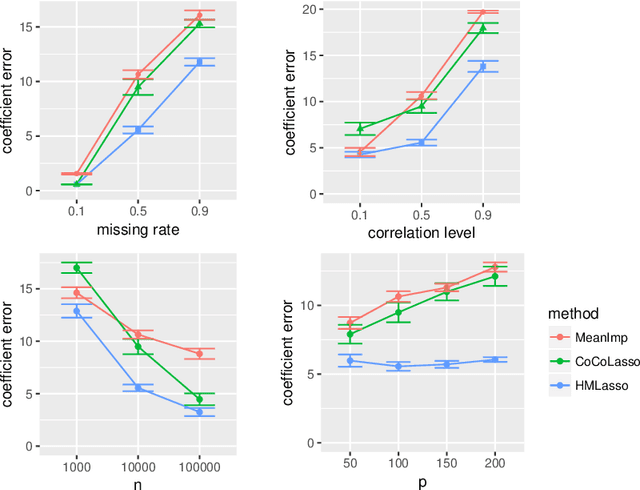
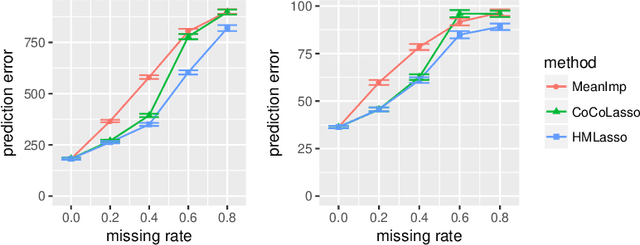
Sparse regression such as Lasso has achieved great success in dealing with high dimensional data for several decades. However, there are few methods applicable to missing data, which often occurs in high dimensional data. Recently, CoCoLasso was proposed to deal with high dimensional missing data, but it still suffers from highly missing data. In this paper, we propose a novel Lasso-type regression technique for Highly Missing data, called `HMLasso'. We use the mean imputed covariance matrix, which is notorious in general due to its estimation bias for missing data. However, we effectively incorporate it into Lasso, by using a useful connection with the pairwise covariance matrix. The resulting optimization problem can be seen as a weighted modification of CoCoLasso with the missing ratios, and is quite effective for highly missing data. To the best of our knowledge, this is the first method that can efficiently deal with both high dimensional and highly missing data. We show that the proposed method is beneficial with regards to non-asymptotic properties of the covariance matrix. Numerical experiments show that the proposed method is highly advantageous in terms of estimation error and generalization error.

Independently Interpretable Lasso: A New Regularizer for Sparse Regression with Uncorrelated Variables

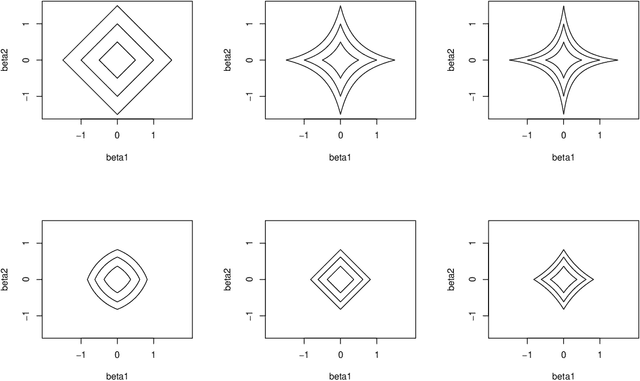
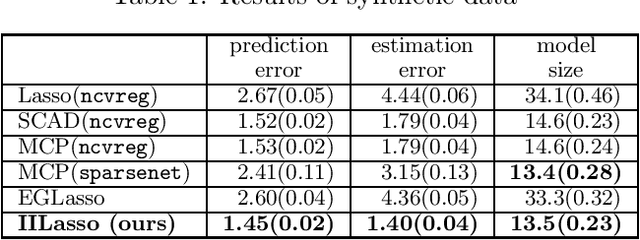
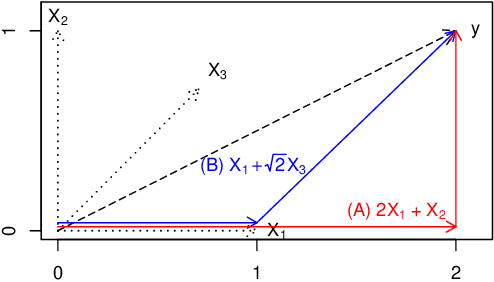
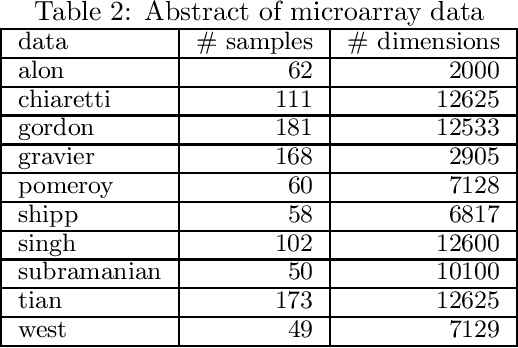
Sparse regularization such as $\ell_1$ regularization is a quite powerful and widely used strategy for high dimensional learning problems. The effectiveness of sparse regularization has been supported practically and theoretically by several studies. However, one of the biggest issues in sparse regularization is that its performance is quite sensitive to correlations between features. Ordinary $\ell_1$ regularization can select variables correlated with each other, which results in deterioration of not only its generalization error but also interpretability. In this paper, we propose a new regularization method, "Independently Interpretable Lasso" (IILasso). Our proposed regularizer suppresses selecting correlated variables, and thus each active variable independently affects the objective variable in the model. Hence, we can interpret regression coefficients intuitively and also improve the performance by avoiding overfitting. We analyze theoretical property of IILasso and show that the proposed method is much advantageous for its sign recovery and achieves almost minimax optimal convergence rate. Synthetic and real data analyses also indicate the effectiveness of IILasso.