Independently Interpretable Lasso: A New Regularizer for Sparse Regression with Uncorrelated Variables
Paper and Code
Feb 22, 2018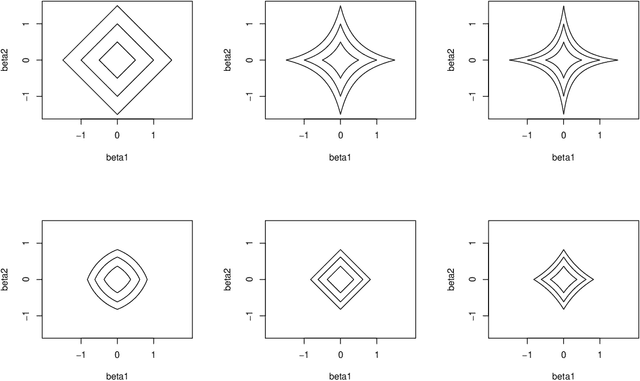
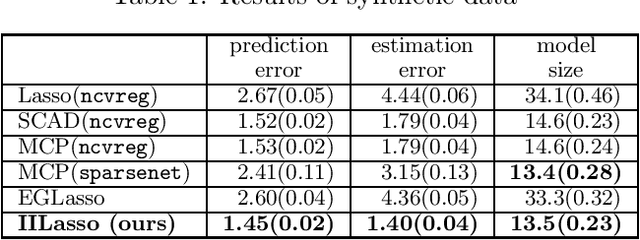
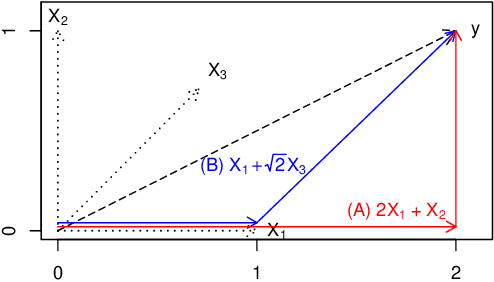
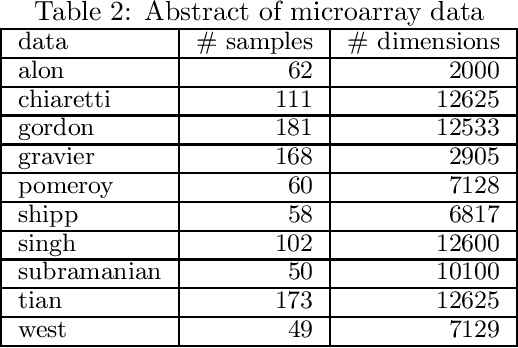
Sparse regularization such as $\ell_1$ regularization is a quite powerful and widely used strategy for high dimensional learning problems. The effectiveness of sparse regularization has been supported practically and theoretically by several studies. However, one of the biggest issues in sparse regularization is that its performance is quite sensitive to correlations between features. Ordinary $\ell_1$ regularization can select variables correlated with each other, which results in deterioration of not only its generalization error but also interpretability. In this paper, we propose a new regularization method, "Independently Interpretable Lasso" (IILasso). Our proposed regularizer suppresses selecting correlated variables, and thus each active variable independently affects the objective variable in the model. Hence, we can interpret regression coefficients intuitively and also improve the performance by avoiding overfitting. We analyze theoretical property of IILasso and show that the proposed method is much advantageous for its sign recovery and achieves almost minimax optimal convergence rate. Synthetic and real data analyses also indicate the effectiveness of IILasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge