HMLasso: Lasso for High Dimensional and Highly Missing Data
Paper and Code
Nov 01, 2018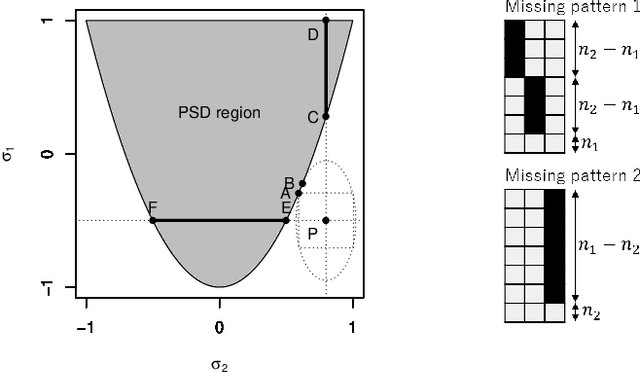
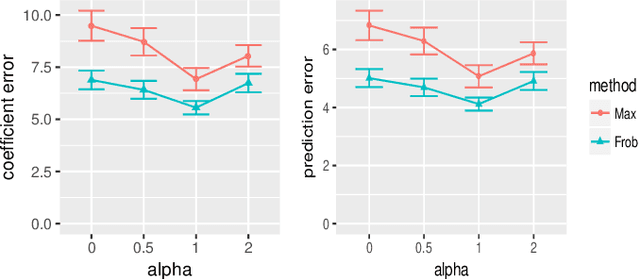
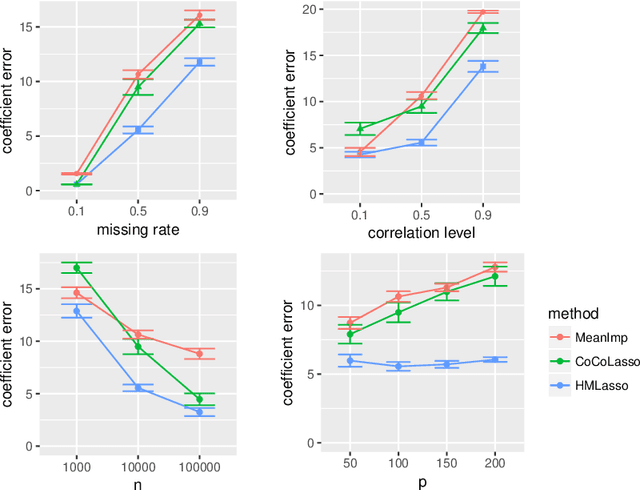
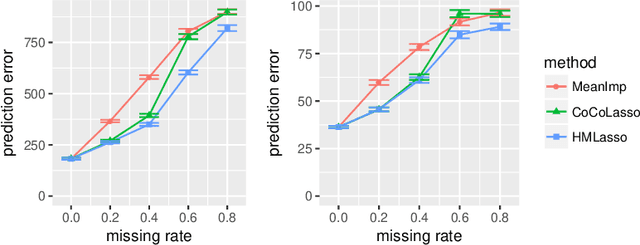
Sparse regression such as Lasso has achieved great success in dealing with high dimensional data for several decades. However, there are few methods applicable to missing data, which often occurs in high dimensional data. Recently, CoCoLasso was proposed to deal with high dimensional missing data, but it still suffers from highly missing data. In this paper, we propose a novel Lasso-type regression technique for Highly Missing data, called `HMLasso'. We use the mean imputed covariance matrix, which is notorious in general due to its estimation bias for missing data. However, we effectively incorporate it into Lasso, by using a useful connection with the pairwise covariance matrix. The resulting optimization problem can be seen as a weighted modification of CoCoLasso with the missing ratios, and is quite effective for highly missing data. To the best of our knowledge, this is the first method that can efficiently deal with both high dimensional and highly missing data. We show that the proposed method is beneficial with regards to non-asymptotic properties of the covariance matrix. Numerical experiments show that the proposed method is highly advantageous in terms of estimation error and generalization error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge