Transfer Learning via $\ell_1$ Regularization
Paper and Code
Jun 26, 2020

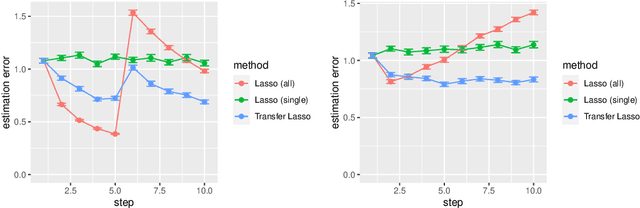
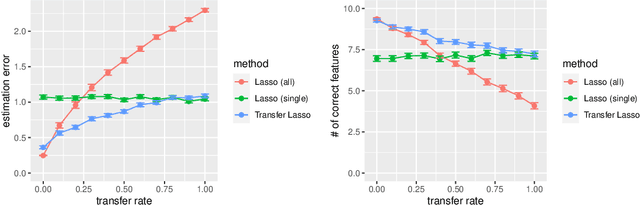
Machine learning algorithms typically require abundant data under a stationary environment. However, environments are nonstationary in many real-world applications. Critical issues lie in how to effectively adapt models under an ever-changing environment. We propose a method for transferring knowledge from a source domain to a target domain via $\ell_1$ regularization. We incorporate $\ell_1$ regularization of differences between source parameters and target parameters, in addition to an ordinary $\ell_1$ regularization. Hence, our method yields sparsity for both the estimates themselves and changes of the estimates. The proposed method has a tight estimation error bound under a stationary environment, and the estimate remains unchanged from the source estimate under small residuals. Moreover, the estimate is consistent with the underlying function, even when the source estimate is mistaken due to nonstationarity. Empirical results demonstrate that the proposed method effectively balances stability and plasticity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge