Robust and Sparse Regression in GLM by Stochastic Optimization
Paper and Code
Feb 09, 2018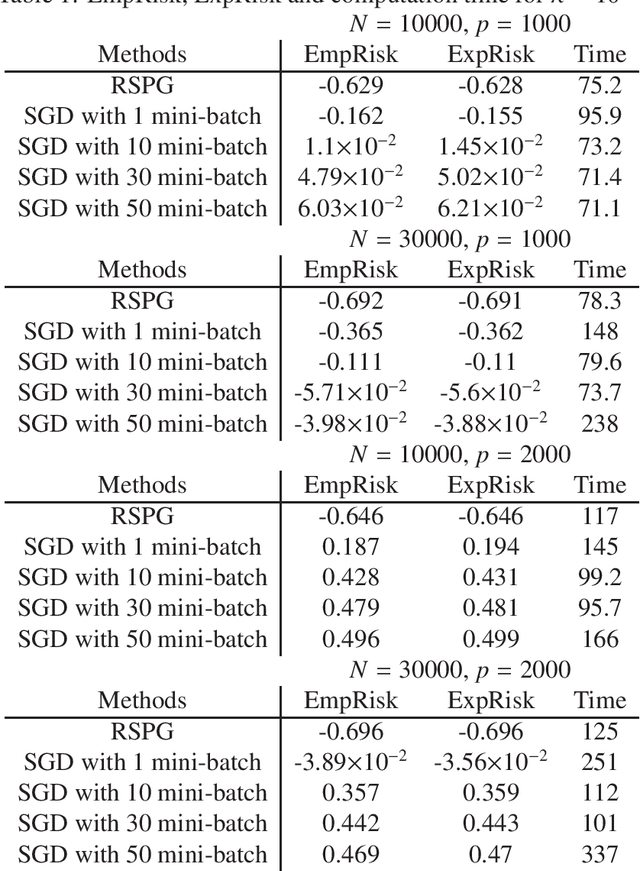



The generalized linear model (GLM) plays a key role in regression analyses. In high-dimensional data, the sparse GLM has been used but it is not robust against outliers. Recently, the robust methods have been proposed for the specific example of the sparse GLM. Among them, we focus on the robust and sparse linear regression based on the $\gamma$-divergence. The estimator of the $\gamma$-divergence has strong robustness under heavy contamination. In this paper, we extend the robust and sparse linear regression based on the $\gamma$-divergence to the robust and sparse GLM based on the $\gamma$-divergence with a stochastic optimization approach in order to obtain the estimate. We adopt the randomized stochastic projected gradient descent as a stochastic optimization approach and extend the established convergence property to the classical first-order necessary condition. By virtue of the stochastic optimization approach, we can efficiently estimate parameters for very large problems. Particularly, we show the linear regression, logistic regression and Poisson regression with $L_1$ regularization in detail as specific examples of robust and sparse GLM. In numerical experiments and real data analysis, the proposed method outperformed comparative methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge