Universal Statistics of Fisher Information in Deep Neural Networks: Mean Field Approach

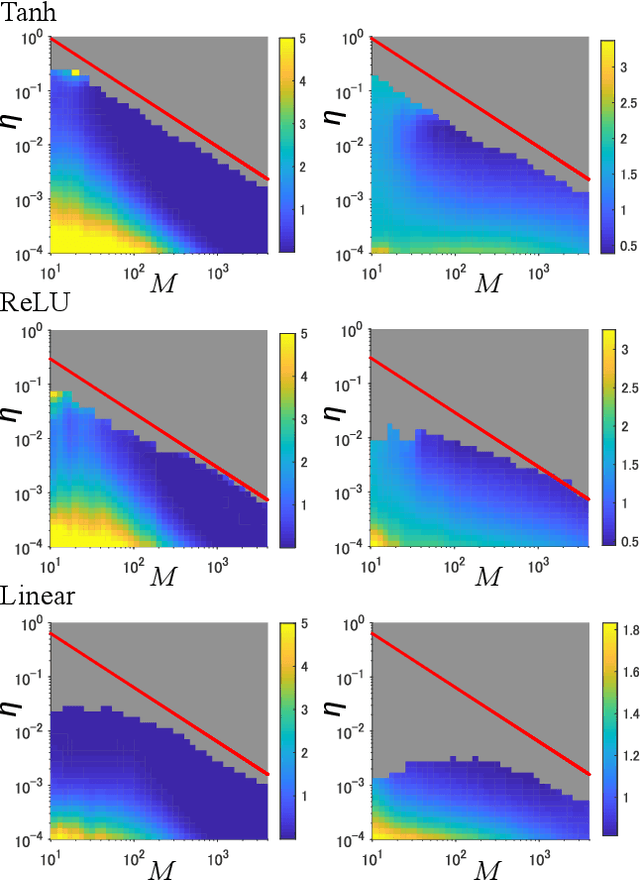
This study analyzes the Fisher information matrix (FIM) by applying mean-field theory to deep neural networks with random weights. We theoretically find novel statistics of the FIM, which are universal among a wide class of deep networks with any number of layers and various activation functions. Although most of the FIM's eigenvalues are close to zero, the maximum eigenvalue takes on a huge value and the eigenvalue distribution has an extremely long tail. These statistics suggest that the shape of a loss landscape is locally flat in most dimensions, but strongly distorted in the other dimensions. Moreover, our theory of the FIM leads to quantitative evaluation of learning in deep networks. First, the maximum eigenvalue enables us to estimate an appropriate size of a learning rate for steepest gradient methods to converge. Second, the flatness induced by the small eigenvalues is connected to generalization ability through a norm-based capacity measure.