Reconsidering Dependency Networks from an Information Geometry Perspective
Paper and Code
Jul 02, 2021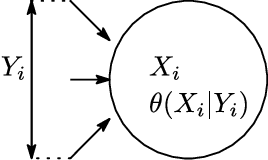
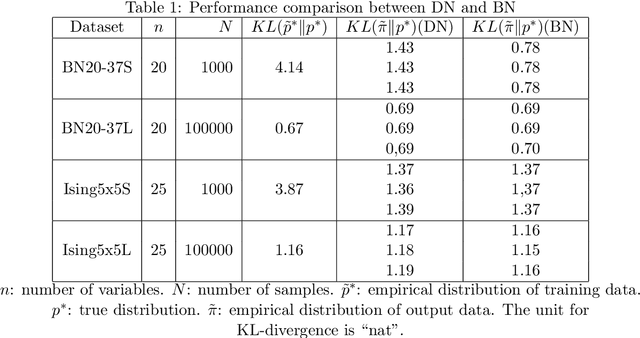
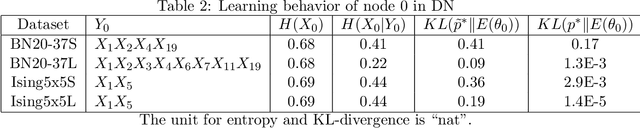
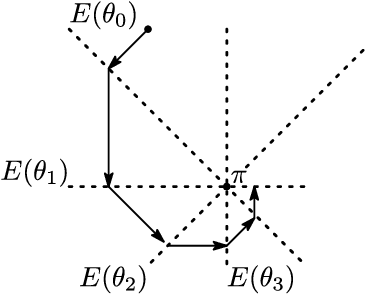
Dependency networks (Heckerman et al., 2000) are potential probabilistic graphical models for systems comprising a large number of variables. Like Bayesian networks, the structure of a dependency network is represented by a directed graph, and each node has a conditional probability table. Learning and inference are realized locally on individual nodes; therefore, computation remains tractable even with a large number of variables. However, the dependency network's learned distribution is the stationary distribution of a Markov chain called pseudo-Gibbs sampling and has no closed-form expressions. This technical disadvantage has impeded the development of dependency networks. In this paper, we consider a certain manifold for each node. Then, we can interpret pseudo-Gibbs sampling as iterative m-projections onto these manifolds. This interpretation provides a theoretical bound for the location where the stationary distribution of pseudo-Gibbs sampling exists in distribution space. Furthermore, this interpretation involves structure and parameter learning algorithms as optimization problems. In addition, we compare dependency and Bayesian networks experimentally. The results demonstrate that the dependency network and the Bayesian network have roughly the same performance in terms of the accuracy of their learned distributions. The results also show that the dependency network can learn much faster than the Bayesian network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge