When Does Preconditioning Help or Hurt Generalization?
Paper and Code
Jul 02, 2020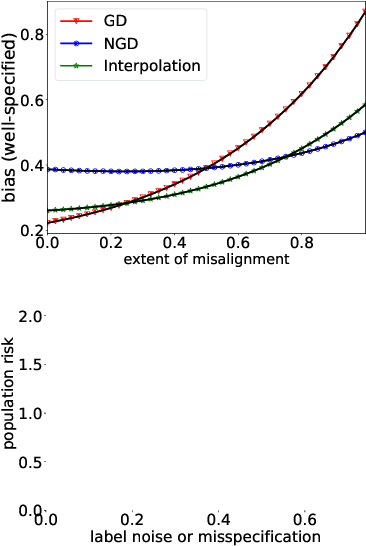
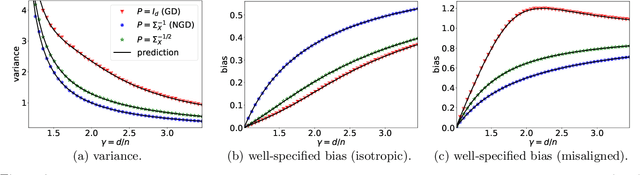

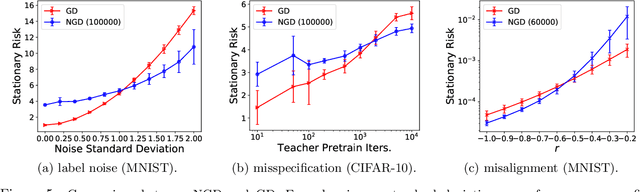
While second order optimizers such as natural gradient descent (NGD) often speed up optimization, their effect on generalization remains controversial. For instance, it has been pointed out that gradient descent (GD), in contrast to many preconditioned updates, converges to small Euclidean norm solutions in overparameterized models, leading to favorable generalization properties. This work presents a more nuanced view on the comparison of generalization between first- and second-order methods. We provide an asymptotic bias-variance decomposition of the generalization error of overparameterized ridgeless regression under a general class of preconditioner $\boldsymbol{P}$, and consider the inverse population Fisher information matrix (used in NGD) as a particular example. We determine the optimal $\boldsymbol{P}$ for both the bias and variance, and find that the relative generalization performance of different optimizers depends on the label noise and the "shape" of the signal (true parameters): when the labels are noisy, the model is misspecified, or the signal is misaligned with the features, NGD can achieve lower risk; conversely, GD generalizes better than NGD under clean labels, a well-specified model, or aligned signal. Based on this analysis, we discuss several approaches to manage the bias-variance tradeoff, and the potential benefit of interpolating between GD and NGD. We then extend our analysis to regression in the reproducing kernel Hilbert space and demonstrate that preconditioned GD can decrease the population risk faster than GD. Lastly, we empirically compare the generalization performance of first- and second-order optimizers in neural network experiments, and observe robust trends matching our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge