Investigating Fine- and Coarse-grained Structural Correspondences Between Deep Neural Networks and Human Object Image Similarity Judgments Using Unsupervised Alignment

The learning mechanisms by which humans acquire internal representations of objects are not fully understood. Deep neural networks (DNNs) have emerged as a useful tool for investigating this question, as they have internal representations similar to those of humans as a byproduct of optimizing their objective functions. While previous studies have shown that models trained with various learning paradigms - such as supervised, self-supervised, and CLIP - acquire human-like representations, it remains unclear whether their similarity to human representations is primarily at a coarse category level or extends to finer details. Here, we employ an unsupervised alignment method based on Gromov-Wasserstein Optimal Transport to compare human and model object representations at both fine-grained and coarse-grained levels. The unique feature of this method compared to conventional representational similarity analysis is that it estimates optimal fine-grained mappings between the representation of each object in human and model representations. We used this unsupervised alignment method to assess the extent to which the representation of each object in humans is correctly mapped to the corresponding representation of the same object in models. Using human similarity judgments of 1,854 objects from the THINGS dataset, we find that models trained with CLIP consistently achieve strong fine- and coarse-grained matching with human object representations. In contrast, self-supervised models showed limited matching at both fine- and coarse-grained levels, but still formed object clusters that reflected human coarse category structure. Our results offer new insights into the role of linguistic information in acquiring precise object representations and the potential of self-supervised learning to capture coarse categorical structures.

Correspondence of high-dimensional emotion structures elicited by video clips between humans and Multimodal LLMs

Recent studies have revealed that human emotions exhibit a high-dimensional, complex structure. A full capturing of this complexity requires new approaches, as conventional models that disregard high dimensionality risk overlooking key nuances of human emotions. Here, we examined the extent to which the latest generation of rapidly evolving Multimodal Large Language Models (MLLMs) capture these high-dimensional, intricate emotion structures, including capabilities and limitations. Specifically, we compared self-reported emotion ratings from participants watching videos with model-generated estimates (e.g., Gemini or GPT). We evaluated performance not only at the individual video level but also from emotion structures that account for inter-video relationships. At the level of simple correlation between emotion structures, our results demonstrated strong similarity between human and model-inferred emotion structures. To further explore whether the similarity between humans and models is at the signle item level or the coarse-categorical level, we applied Gromov Wasserstein Optimal Transport. We found that although performance was not necessarily high at the strict, single-item level, performance across video categories that elicit similar emotions was substantial, indicating that the model could infer human emotional experiences at the category level. Our results suggest that current state-of-the-art MLLMs broadly capture the complex high-dimensional emotion structures at the category level, as well as their apparent limitations in accurately capturing entire structures at the single-item level.

Constructive Approach to Bidirectional Causation between Qualia Structure and Language Emergence

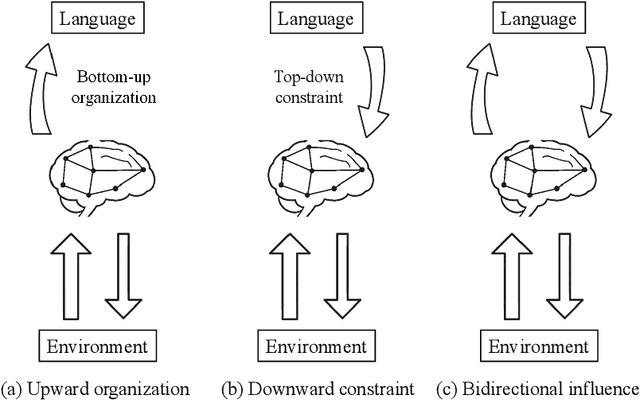
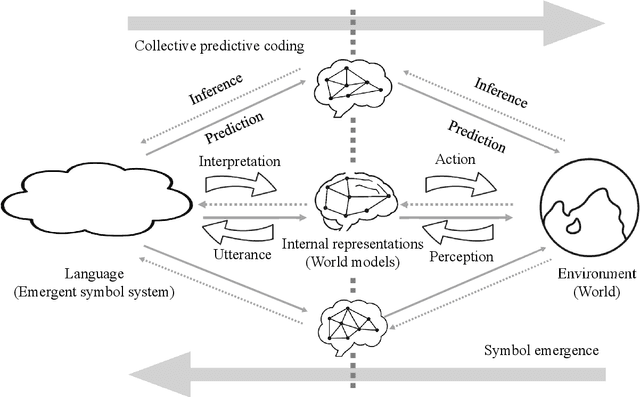
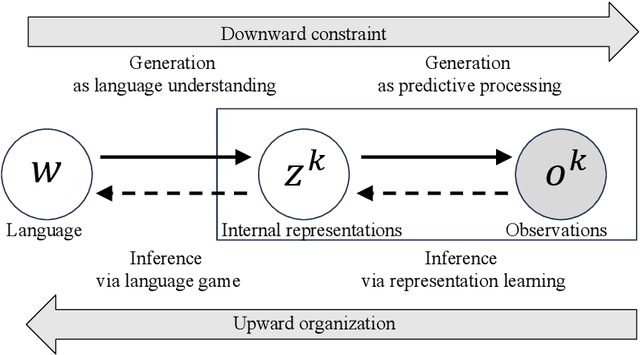
This paper presents a novel perspective on the bidirectional causation between language emergence and relational structure of subjective experiences, termed qualia structure, and lays out the constructive approach to the intricate dependency between the two. We hypothesize that languages with distributional semantics, e.g., syntactic-semantic structures, may have emerged through the process of aligning internal representations among individuals, and such alignment of internal representations facilitates more structured language. This mutual dependency is suggested by the recent advancements in AI and symbol emergence robotics, and collective predictive coding (CPC) hypothesis, in particular. Computational studies show that neural network-based language models form systematically structured internal representations, and multimodal language models can share representations between language and perceptual information. This perspective suggests that language emergence serves not only as a mechanism creating a communication tool but also as a mechanism for allowing people to realize shared understanding of qualitative experiences. The paper discusses the implications of this bidirectional causation in the context of consciousness studies, linguistics, and cognitive science, and outlines future constructive research directions to further explore this dynamic relationship between language emergence and qualia structure.

Fisher Information and Natural Gradient Learning of Random Deep Networks

A deep neural network is a hierarchical nonlinear model transforming input signals to output signals. Its input-output relation is considered to be stochastic, being described for a given input by a parameterized conditional probability distribution of outputs. The space of parameters consisting of weights and biases is a Riemannian manifold, where the metric is defined by the Fisher information matrix. The natural gradient method uses the steepest descent direction in a Riemannian manifold, so it is effective in learning, avoiding plateaus. It requires inversion of the Fisher information matrix, however, which is practically impossible when the matrix has a huge number of dimensions. Many methods for approximating the natural gradient have therefore been introduced. The present paper uses statistical neurodynamical method to reveal the properties of the Fisher information matrix in a net of random connections under the mean field approximation. We prove that the Fisher information matrix is unit-wise block diagonal supplemented by small order terms of off-block-diagonal elements, which provides a justification for the quasi-diagonal natural gradient method by Y. Ollivier. A unitwise block-diagonal Fisher metrix reduces to the tensor product of the Fisher information matrices of single units. We further prove that the Fisher information matrix of a single unit has a simple reduced form, a sum of a diagonal matrix and a rank 2 matrix of weight-bias correlations. We obtain the inverse of Fisher information explicitly. We then have an explicit form of the natural gradient, without relying on the numerical matrix inversion, which drastically speeds up stochastic gradient learning.

Statistical Neurodynamics of Deep Networks: Geometry of Signal Spaces

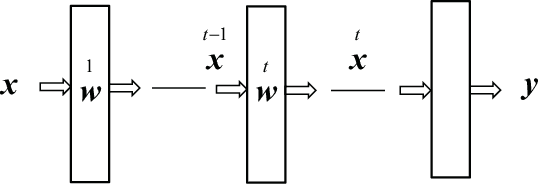
Statistical neurodynamics studies macroscopic behaviors of randomly connected neural networks. We consider a deep layered feedforward network where input signals are processed layer by layer. The manifold of input signals is embedded in a higher dimensional manifold of the next layer as a curved submanifold, provided the number of neurons is larger than that of inputs. We show geometrical features of the embedded manifold, proving that the manifold enlarges or shrinks locally isotropically so that it is always embedded conformally. We study the curvature of the embedded manifold. The scalar curvature converges to a constant or diverges to infinity slowly. The distance between two signals also changes, converging eventually to a stable fixed value, provided both the number of neurons in a layer and the number of layers tend to infinity. This causes a problem, since when we consider a curve in the input space, it is mapped as a continuous curve of fractal nature, but our theory contradictorily suggests that the curve eventually converges to a discrete set of equally spaced points. In reality, the numbers of neurons and layers are finite and thus, it is expected that the finite size effect causes the discrepancies between our theory and reality. We need to further study the discrepancies to understand their implications on information processing.

Efficient Algorithms for Searching the Minimum Information Partition in Integrated Information Theory

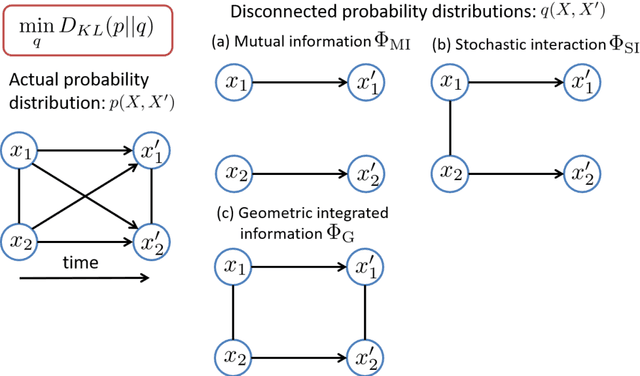
The ability to integrate information in the brain is considered to be an essential property for cognition and consciousness. Integrated Information Theory (IIT) hypothesizes that the amount of integrated information ($\Phi$) in the brain is related to the level of consciousness. IIT proposes that to quantify information integration in a system as a whole, integrated information should be measured across the partition of the system at which information loss caused by partitioning is minimized, called the Minimum Information Partition (MIP). The computational cost for exhaustively searching for the MIP grows exponentially with system size, making it difficult to apply IIT to real neural data. It has been previously shown that if a measure of $\Phi$ satisfies a mathematical property, submodularity, the MIP can be found in a polynomial order by an optimization algorithm. However, although the first version of $\Phi$ is submodular, the later versions are not. In this study, we empirically explore to what extent the algorithm can be applied to the non-submodular measures of $\Phi$ by evaluating the accuracy of the algorithm in simulated data and real neural data. We find that the algorithm identifies the MIP in a nearly perfect manner even for the non-submodular measures. Our results show that the algorithm allows us to measure $\Phi$ in large systems within a practical amount of time.