Jun Kitazono
Efficient Algorithms for Searching the Minimum Information Partition in Integrated Information Theory
Feb 13, 2018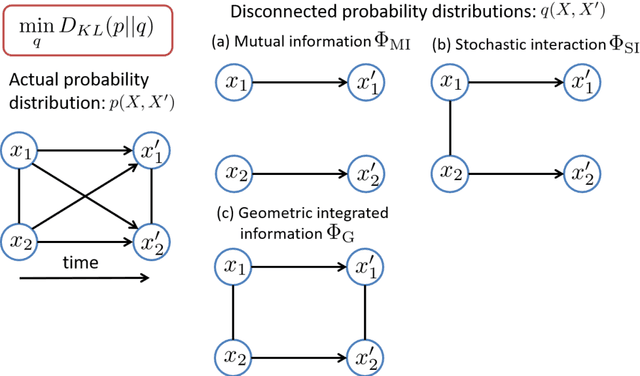



Abstract:The ability to integrate information in the brain is considered to be an essential property for cognition and consciousness. Integrated Information Theory (IIT) hypothesizes that the amount of integrated information ($\Phi$) in the brain is related to the level of consciousness. IIT proposes that to quantify information integration in a system as a whole, integrated information should be measured across the partition of the system at which information loss caused by partitioning is minimized, called the Minimum Information Partition (MIP). The computational cost for exhaustively searching for the MIP grows exponentially with system size, making it difficult to apply IIT to real neural data. It has been previously shown that if a measure of $\Phi$ satisfies a mathematical property, submodularity, the MIP can be found in a polynomial order by an optimization algorithm. However, although the first version of $\Phi$ is submodular, the later versions are not. In this study, we empirically explore to what extent the algorithm can be applied to the non-submodular measures of $\Phi$ by evaluating the accuracy of the algorithm in simulated data and real neural data. We find that the algorithm identifies the MIP in a nearly perfect manner even for the non-submodular measures. Our results show that the algorithm allows us to measure $\Phi$ in large systems within a practical amount of time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge