Causal Autoregressive Flows

Two apparently unrelated fields -- normalizing flows and causality -- have recently received considerable attention in the machine learning community. In this work, we highlight an intrinsic correspondence between a simple family of flows and identifiable causal models. We exploit the fact that autoregressive flow architectures define an ordering over variables, analogous to a causal ordering, to show that they are well-suited to performing a range of causal inference tasks. First, we show that causal models derived from both affine and additive flows are identifiable. This provides a generalization of the additive noise model well-known in causal discovery. Second, we derive a bivariate measure of causal direction based on likelihood ratios, leveraging the fact that flow models estimate normalized log-densities of data. Such likelihood ratios have well-known optimality properties in finite-sample inference. Third, we demonstrate that the invertibility of flows naturally allows for direct evaluation of both interventional and counterfactual queries. Finally, throughout a series of experiments on synthetic and real data, the proposed method is shown to outperform current approaches for causal discovery as well as making accurate interventional and counterfactual predictions.

Autoregressive flow-based causal discovery and inference

We posit that autoregressive flow models are well-suited to performing a range of causal inference tasks - ranging from causal discovery to making interventional and counterfactual predictions. In particular, we exploit the fact that autoregressive architectures define an ordering over variables, analogous to a causal ordering, in order to propose a single flow architecture to perform all three aforementioned tasks. We first leverage the fact that flow models estimate normalized log-densities of data to derive a bivariate measure of causal direction based on likelihood ratios. Whilst traditional measures of causal direction often require restrictive assumptions on the nature of causal relationships (e.g., linearity),the flexibility of flow models allows for arbitrary causal dependencies. Our approach compares favourably against alternative methods on synthetic data as well as on the Cause-Effect Pairs bench-mark dataset. Subsequently, we demonstrate that the invertible nature of flows naturally allows for direct evaluation of both interventional and counterfactual predictions, which require marginalization and conditioning over latent variables respectively. We present examples over synthetic data where autoregressive flows, when trained under the correct causal ordering, are able to make accurate interventional and counterfactual predictions

Bayesian optimization for automatic design of face stimuli

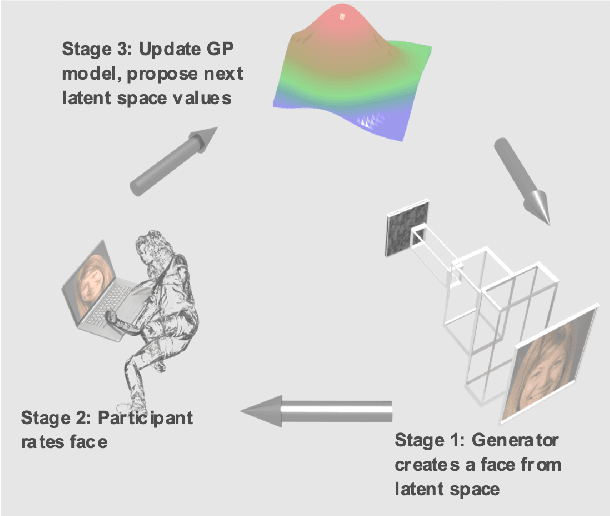
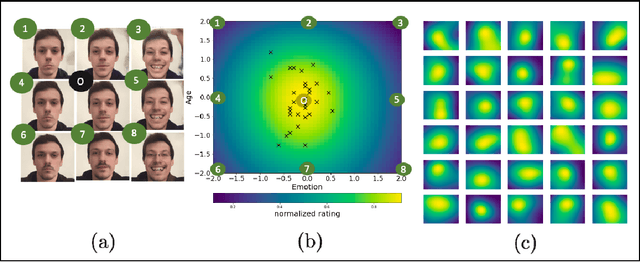
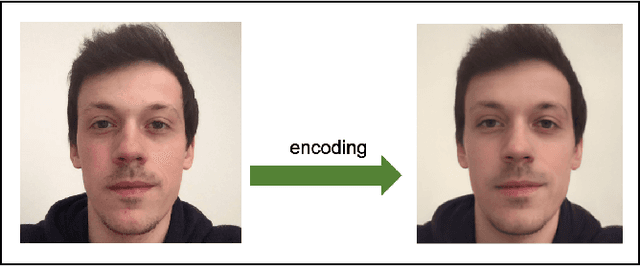
Investigating the cognitive and neural mechanisms involved with face processing is a fundamental task in modern neuroscience and psychology. To date, the majority of such studies have focused on the use of pre-selected stimuli. The absence of personalized stimuli presents a serious limitation as it fails to account for how each individual face processing system is tuned to cultural embeddings or how it is disrupted in disease. In this work, we propose a novel framework which combines generative adversarial networks (GANs) with Bayesian optimization to identify individual response patterns to many different faces. Formally, we employ Bayesian optimization to efficiently search the latent space of state-of-the-art GAN models, with the aim to automatically generate novel faces, to maximize an individual subject's response. We present results from a web-based proof-of-principle study, where participants rated images of themselves generated via performing Bayesian optimization over the latent space of a GAN. We show how the algorithm can efficiently locate an individual's optimal face while mapping out their response across different semantic transformations of a face; inter-individual analyses suggest how the approach can provide rich information about individual differences in face processing.

ICE-BeeM: Identifiable Conditional Energy-Based Deep Models

Despite the growing popularity of energy-based models, their identifiability properties are not well-understood. In this paper we establish sufficient conditions under which a large family of conditional energy-based models is identifiable in function space, up to a simple transformation. Our results build on recent developments in the theory of nonlinear ICA, showing that the latent representations in certain families of deep latent-variable models are identifiable. We extend these results to a very broad family of conditional energy-based models. In this family, the energy function is simply the dot-product between two feature extractors, one for the dependent variable, and one for the conditioning variable. We show that under mild conditions, the features are unique up to scaling and permutation. Second, we propose the framework of independently modulated component analysis (IMCA), a new form of nonlinear ICA where the indepencence assumption is relaxed. Importantly, we show that our energy-based model can be used for the estimation of the components: the features learned are a simple and often trivial transformation of the latents.

Causal Discovery with General Non-Linear Relationships Using Non-Linear ICA

We consider the problem of inferring causal relationships between two or more passively observed variables. While the problem of such causal discovery has been extensively studied especially in the bivariate setting, the majority of current methods assume a linear causal relationship, and the few methods which consider non-linear dependencies usually make the assumption of additive noise. Here, we propose a framework through which we can perform causal discovery in the presence of general non-linear relationships. The proposed method is based on recent progress in non-linear independent component analysis and exploits the non-stationarity of observations in order to recover the underlying sources or latent disturbances. We show rigorously that in the case of bivariate causal discovery, such non-linear ICA can be used to infer the causal direction via a series of independence tests. We further propose an alternative measure of causal direction based on asymptotic approximations to the likelihood ratio, as well as an extension to multivariate causal discovery. We demonstrate the capabilities of the proposed method via a series of simulation studies and conclude with an application to neuroimaging data.

A Unified Probabilistic Model for Learning Latent Factors and Their Connectivities from High-Dimensional Data

Connectivity estimation is challenging in the context of high-dimensional data. A useful preprocessing step is to group variables into clusters, however, it is not always clear how to do so from the perspective of connectivity estimation. Another practical challenge is that we may have data from multiple related classes (e.g., multiple subjects or conditions) and wish to incorporate constraints on the similarities across classes. We propose a probabilistic model which simultaneously performs both a grouping of variables (i.e., detecting community structure) and estimation of connectivities between the groups which correspond to latent variables. The model is essentially a factor analysis model where the factors are allowed to have arbitrary correlations, while the factor loading matrix is constrained to express a community structure. The model can be applied on multiple classes so that the connectivities can be different between the classes, while the community structure is the same for all classes. We propose an efficient estimation algorithm based on score matching, and prove the identifiability of the model. Finally, we present an extension to directed (causal) connectivities over latent variables. Simulations and experiments on fMRI data validate the practical utility of the method.

Adaptive regularization for Lasso models in the context of non-stationary data streams

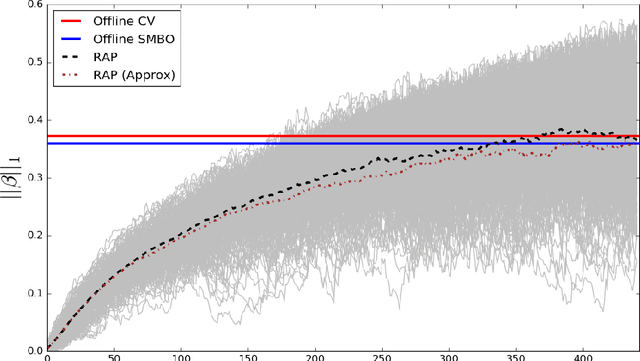
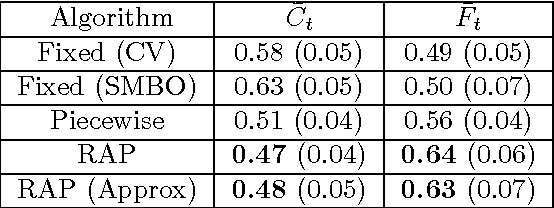
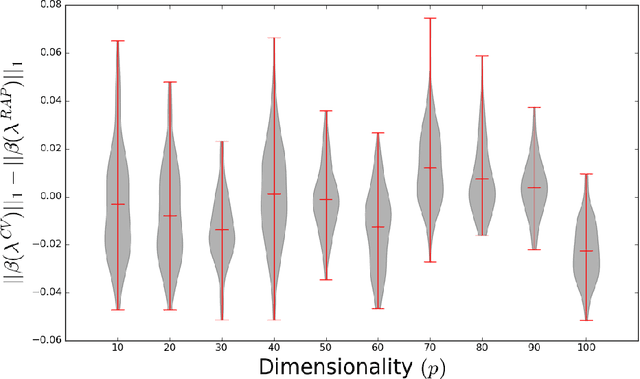
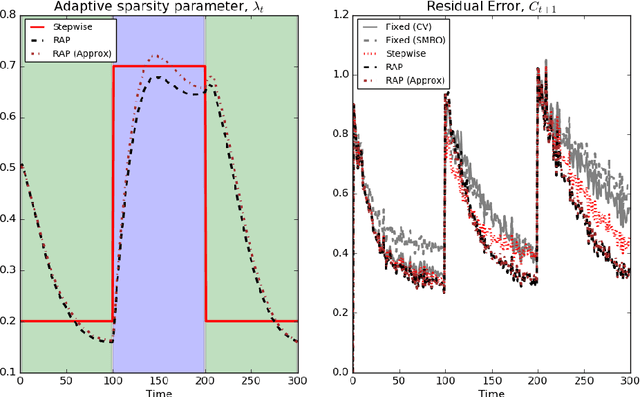
Large scale, streaming datasets are ubiquitous in modern machine learning. Streaming algorithms must be scalable, amenable to incremental training and robust to the presence of non-stationarity. In this work consider the problem of learning $\ell_1$ regularized linear models in the context of streaming data. In particular, the focus of this work revolves around how to select the regularization parameter when data arrives sequentially and the underlying distribution is non-stationary (implying the choice of optimal regularization parameter is itself time-varying). We propose a framework through which to infer an adaptive regularization parameter. Our approach employs an $\ell_1$ penalty constraint where the corresponding sparsity parameter is iteratively updated via stochastic gradient descent. This serves to reformulate the choice of regularization parameter in a principled framework for online learning. The proposed method is derived for linear regression and subsequently extended to generalized linear models. We validate our approach using simulated and real datasets and present an application to a neuroimaging dataset.

Streaming regularization parameter selection via stochastic gradient descent

We propose a framework to perform streaming covariance selection. Our approach employs regularization constraints where a time-varying sparsity parameter is iteratively estimated via stochastic gradient descent. This allows for the regularization parameter to be efficiently learnt in an online manner. The proposed framework is developed for linear regression models and extended to graphical models via neighbourhood selection. Under mild assumptions, we are able to obtain convergence results in a non-stochastic setting. The capabilities of such an approach are demonstrated using both synthetic data as well as neuroimaging data.

Text-mining the NeuroSynth corpus using Deep Boltzmann Machines

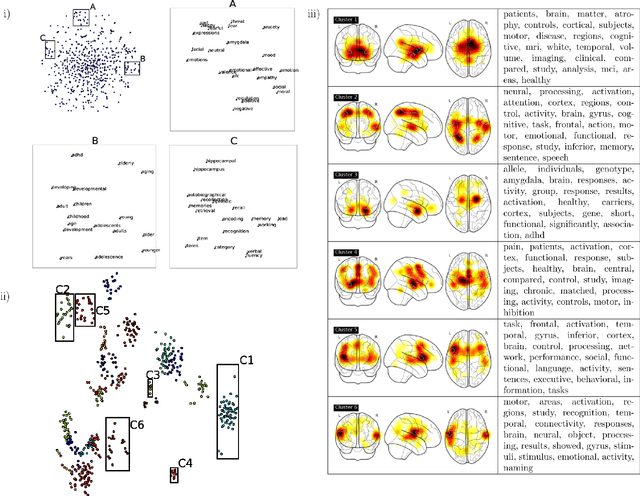
Large-scale automated meta-analysis of neuroimaging data has recently established itself as an important tool in advancing our understanding of human brain function. This research has been pioneered by NeuroSynth, a database collecting both brain activation coordinates and associated text across a large cohort of neuroimaging research papers. One of the fundamental aspects of such meta-analysis is text-mining. To date, word counts and more sophisticated methods such as Latent Dirichlet Allocation have been proposed. In this work we present an unsupervised study of the NeuroSynth text corpus using Deep Boltzmann Machines (DBMs). The use of DBMs yields several advantages over the aforementioned methods, principal among which is the fact that it yields both word and document embeddings in a high-dimensional vector space. Such embeddings serve to facilitate the use of traditional machine learning techniques on the text corpus. The proposed DBM model is shown to learn embeddings with a clear semantic structure.

Learning population and subject-specific brain connectivity networks via Mixed Neighborhood Selection

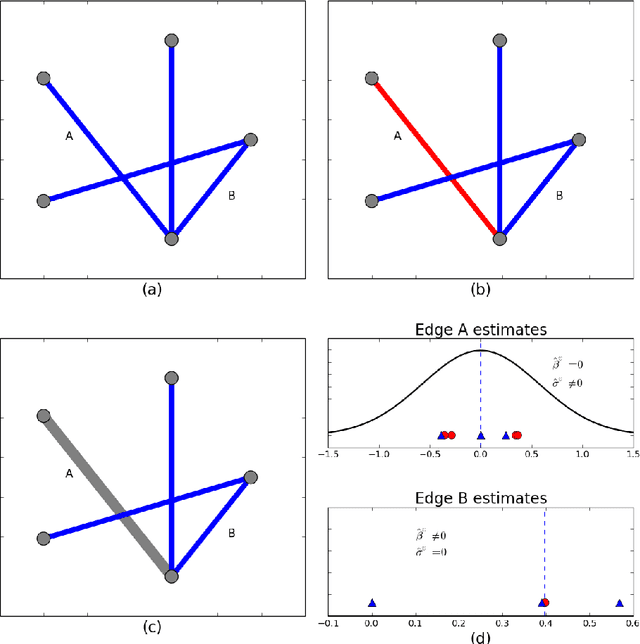
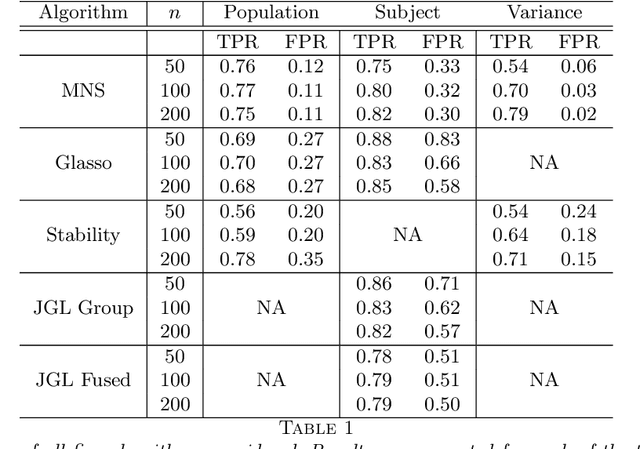
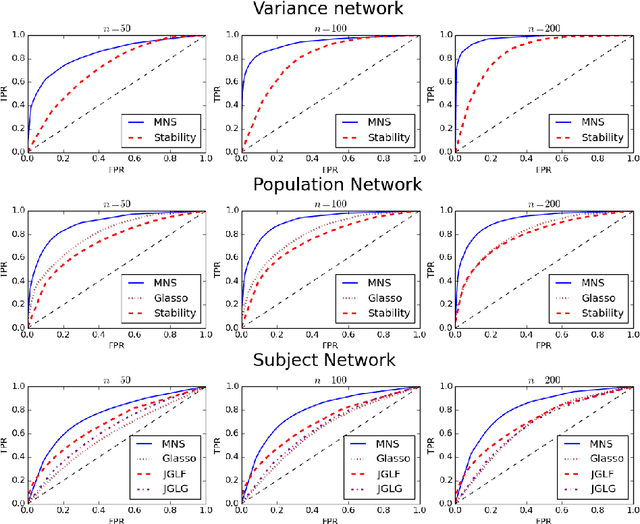
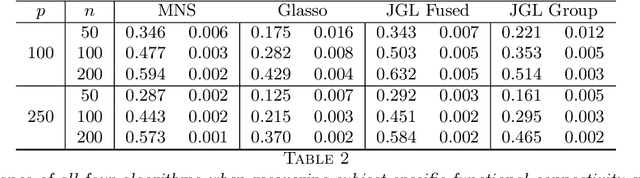
In neuroimaging data analysis, Gaussian graphical models are often used to model statistical dependencies across spatially remote brain regions known as functional connectivity. Typically, data is collected across a cohort of subjects and the scientific objectives consist of estimating population and subject-specific graphical models. A third objective that is often overlooked involves quantifying inter-subject variability and thus identifying regions or sub-networks that demonstrate heterogeneity across subjects. Such information is fundamental in order to thoroughly understand the human connectome. We propose Mixed Neighborhood Selection in order to simultaneously address the three aforementioned objectives. By recasting covariance selection as a neighborhood selection problem we are able to efficiently learn the topology of each node. We introduce an additional mixed effect component to neighborhood selection in order to simultaneously estimate a graphical model for the population of subjects as well as for each individual subject. The proposed method is validated empirically through a series of simulations and applied to resting state data for healthy subjects taken from the ABIDE consortium.