Learning population and subject-specific brain connectivity networks via Mixed Neighborhood Selection
Paper and Code
Dec 07, 2015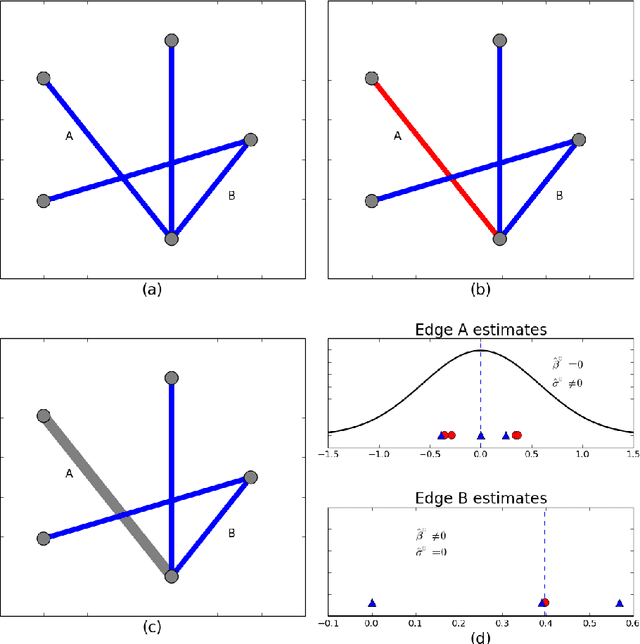
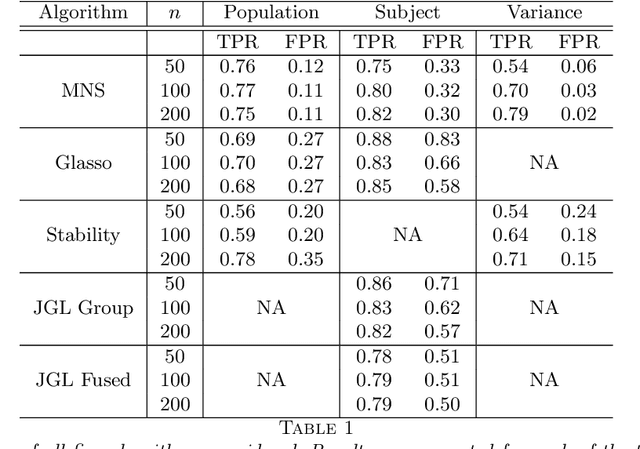
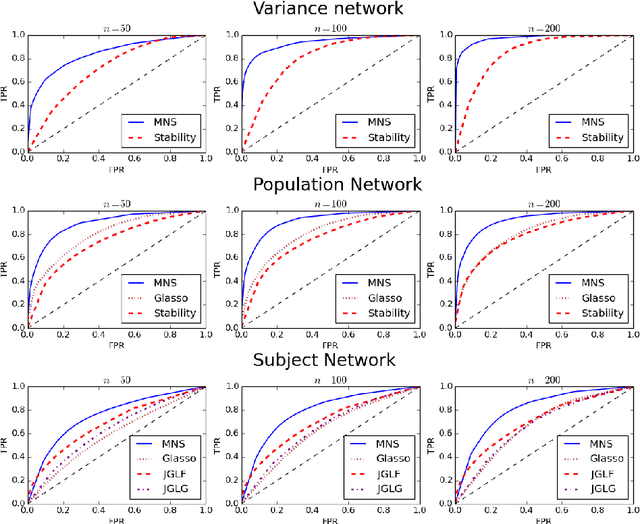
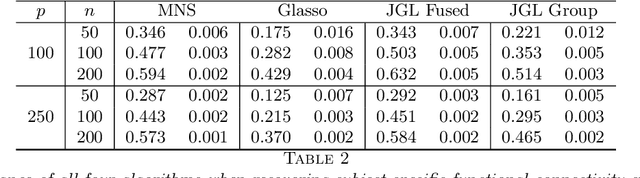
In neuroimaging data analysis, Gaussian graphical models are often used to model statistical dependencies across spatially remote brain regions known as functional connectivity. Typically, data is collected across a cohort of subjects and the scientific objectives consist of estimating population and subject-specific graphical models. A third objective that is often overlooked involves quantifying inter-subject variability and thus identifying regions or sub-networks that demonstrate heterogeneity across subjects. Such information is fundamental in order to thoroughly understand the human connectome. We propose Mixed Neighborhood Selection in order to simultaneously address the three aforementioned objectives. By recasting covariance selection as a neighborhood selection problem we are able to efficiently learn the topology of each node. We introduce an additional mixed effect component to neighborhood selection in order to simultaneously estimate a graphical model for the population of subjects as well as for each individual subject. The proposed method is validated empirically through a series of simulations and applied to resting state data for healthy subjects taken from the ABIDE consortium.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge