Model Free Prediction with Uncertainty Assessment

Deep nonparametric regression, characterized by the utilization of deep neural networks to learn target functions, has emerged as a focal point of research attention in recent years. Despite considerable progress in understanding convergence rates, the absence of asymptotic properties hinders rigorous statistical inference. To address this gap, we propose a novel framework that transforms the deep estimation paradigm into a platform conducive to conditional mean estimation, leveraging the conditional diffusion model. Theoretically, we develop an end-to-end convergence rate for the conditional diffusion model and establish the asymptotic normality of the generated samples. Consequently, we are equipped to construct confidence regions, facilitating robust statistical inference. Furthermore, through numerical experiments, we empirically validate the efficacy of our proposed methodology.

Latent Schr{ö}dinger Bridge Diffusion Model for Generative Learning

This paper aims to conduct a comprehensive theoretical analysis of current diffusion models. We introduce a novel generative learning methodology utilizing the Schr{\"o}dinger bridge diffusion model in latent space as the framework for theoretical exploration in this domain. Our approach commences with the pre-training of an encoder-decoder architecture using data originating from a distribution that may diverge from the target distribution, thus facilitating the accommodation of a large sample size through the utilization of pre-existing large-scale models. Subsequently, we develop a diffusion model within the latent space utilizing the Schr{\"o}dinger bridge framework. Our theoretical analysis encompasses the establishment of end-to-end error analysis for learning distributions via the latent Schr{\"o}dinger bridge diffusion model. Specifically, we control the second-order Wasserstein distance between the generated distribution and the target distribution. Furthermore, our obtained convergence rates effectively mitigate the curse of dimensionality, offering robust theoretical support for prevailing diffusion models.

An empirical study of the effect of background data size on the stability of SHapley Additive exPlanations for deep learning models

Nowadays, the interpretation of why a machine learning (ML) model makes certain inferences is as crucial as the accuracy of such inferences. Some ML models like the decision tree possess inherent interpretability that can be directly comprehended by humans. Others like artificial neural networks (ANN), however, rely on external methods to uncover the deduction mechanism. SHapley Additive exPlanations (SHAP) is one of such external methods, which requires a background dataset when interpreting ANNs. Generally, a background dataset consists of instances randomly sampled from the training dataset. However, the sampling size and its effect on SHAP remain to be unexplored. In our empirical study on the MIMIC-III dataset, we show that the two core explanations - SHAP values and variable rankings fluctuate when using different background datasets acquired from random sampling, indicating that users cannot unquestioningly trust the one-shot interpretation from SHAP. Luckily, such fluctuation decreases with the increase of the background dataset size. Also, we notice an U-shape in the stability assessment of SHAP variable rankings, demonstrating that SHAP is more reliable in ranking the most and least important variables compared to moderately important ones. Overall, our results suggest that users should take into account how background data affects SHAP results, with improved SHAP stability as the background sample size increases.

A Data-Driven Line Search Rule for Support Recovery in High-dimensional Data Analysis

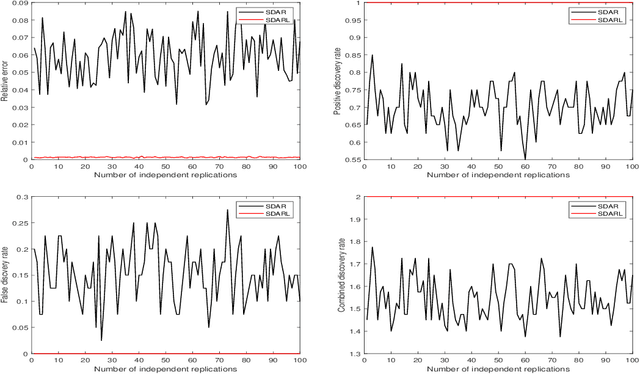
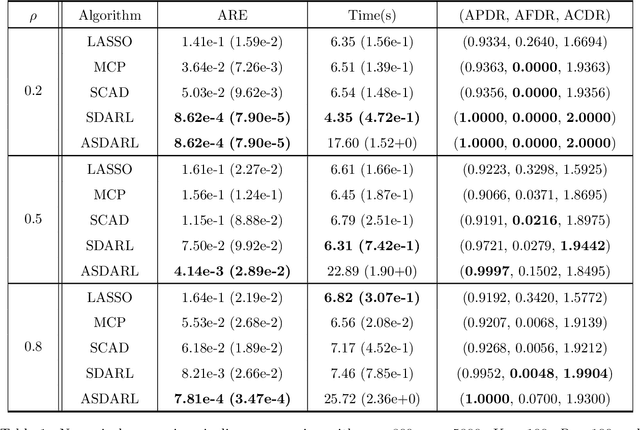
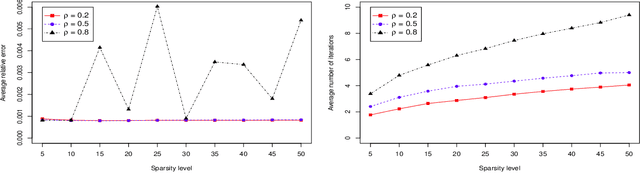
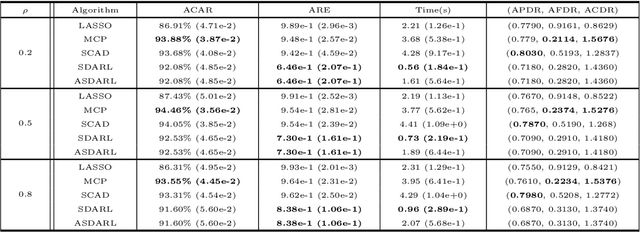
In this work, we consider the algorithm to the (nonlinear) regression problems with $\ell_0$ penalty. The existing algorithms for $\ell_0$ based optimization problem are often carried out with a fixed step size, and the selection of an appropriate step size depends on the restricted strong convexity and smoothness for the loss function, hence it is difficult to compute in practical calculation. In sprite of the ideas of support detection and root finding \cite{HJK2020}, we proposes a novel and efficient data-driven line search rule to adaptively determine the appropriate step size. We prove the $\ell_2$ error bound to the proposed algorithm without much restrictions for the cost functional. A large number of numerical comparisons with state-of-the-art algorithms in linear and logistic regression problems show the stability, effectiveness and superiority of the proposed algorithms.

Convergence Analysis of Schr{ö}dinger-F{ö}llmer Sampler without Convexity

Schr\"{o}dinger-F\"{o}llmer sampler (SFS) is a novel and efficient approach for sampling from possibly unnormalized distributions without ergodicity. SFS is based on the Euler-Maruyama discretization of Schr\"{o}dinger-F\"{o}llmer diffusion process $$\mathrm{d} X_{t}=-\nabla U\left(X_t, t\right) \mathrm{d} t+\mathrm{d} B_{t}, \quad t \in[0,1],\quad X_0=0$$ on the unit interval, which transports the degenerate distribution at time zero to the target distribution at time one. In \cite{sfs21}, the consistency of SFS is established under a restricted assumption that %the drift term $b(x,t)$ the potential $U(x,t)$ is uniformly (on $t$) strongly %concave convex (on $x$). In this paper we provide a nonasymptotic error bound of SFS in Wasserstein distance under some smooth and bounded conditions on the density ratio of the target distribution over the standard normal distribution, but without requiring the strongly convexity of the potential.

On Newton Screening

Screening and working set techniques are important approaches to reducing the size of an optimization problem. They have been widely used in accelerating first-order methods for solving large-scale sparse learning problems. In this paper, we develop a new screening method called Newton screening (NS) which is a generalized Newton method with a built-in screening mechanism. We derive an equivalent KKT system for the Lasso and utilize a generalized Newton method to solve the KKT equations. Based on this KKT system, a built-in working set with a relatively small size is first determined using the sum of primal and dual variables generated from the previous iteration, then the primal variable is updated by solving a least-squares problem on the working set and the dual variable updated based on a closed-form expression. Moreover, we consider a sequential version of Newton screening (SNS) with a warm-start strategy. We show that NS possesses an optimal convergence property in the sense that it achieves one-step local convergence. Under certain regularity conditions on the feature matrix, we show that SNS hits a solution with the same signs as the underlying true target and achieves a sharp estimation error bound with high probability. Simulation studies and real data analysis support our theoretical results and demonstrate that SNS is faster and more accurate than several state-of-the-art methods in our comparative studies.

A Support Detection and Root Finding Approach for Learning High-dimensional Generalized Linear Models

Feature selection is important for modeling high-dimensional data, where the number of variables can be much larger than the sample size. In this paper, we develop a support detection and root finding procedure to learn the high dimensional sparse generalized linear models and denote this method by GSDAR. Based on the KKT condition for $\ell_0$-penalized maximum likelihood estimations, GSDAR generates a sequence of estimators iteratively. Under some restricted invertibility conditions on the maximum likelihood function and sparsity assumption on the target coefficients, the errors of the proposed estimate decays exponentially to the optimal order. Moreover, the oracle estimator can be recovered if the target signal is stronger than the detectable level. We conduct simulations and real data analysis to illustrate the advantages of our proposed method over several existing methods, including Lasso and MCP.