Huazhen Lin
Olica: Efficient Structured Pruning of Large Language Models without Retraining
Jun 10, 2025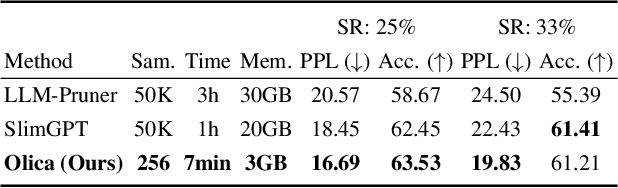
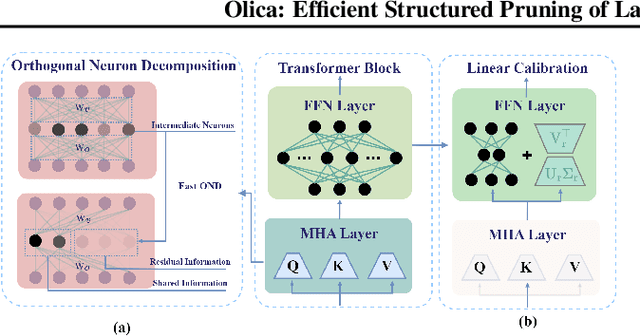
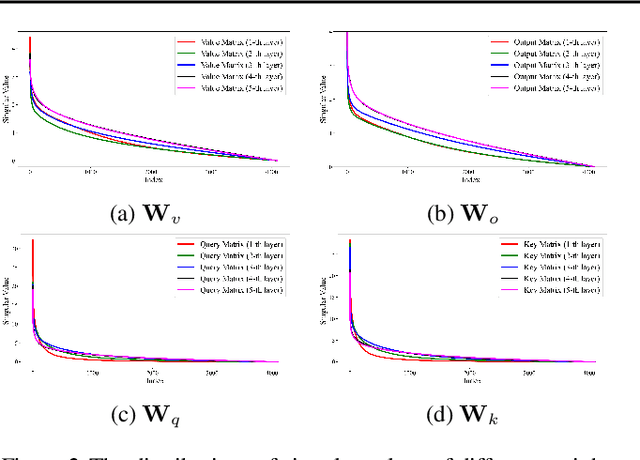
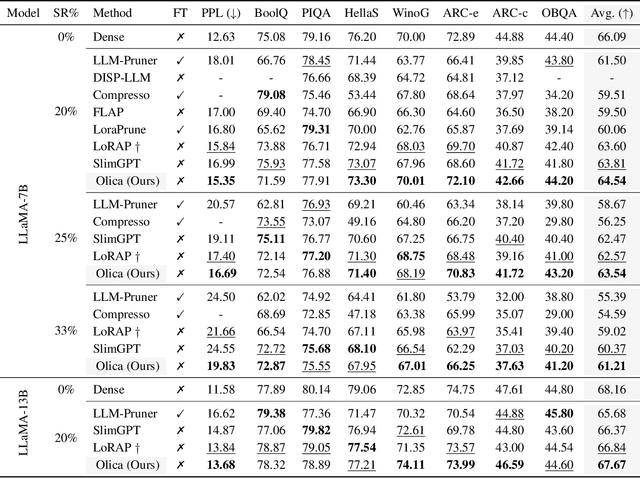
Abstract:Most existing structured pruning methods for Large Language Models (LLMs) require substantial computational and data resources for retraining to reestablish the corrupted correlations, making them prohibitively expensive. To address this, we propose a pruning framework for LLMs called Orthogonal decomposition and Linear Calibration (Olica), which eliminates the need for retraining. A key observation is that the multi-head attention (MHA) layer depends on two types of matrix products. By treating these matrix products as unified entities and applying principal component analysis (PCA), we extract the most important information to compress LLMs without sacrificing accuracy or disrupting their original structure. Consequently, retraining becomes unnecessary. A fast decomposition method is devised, reducing the complexity of PCA by a factor of the square of the number of attention heads. Additionally, to mitigate error accumulation problem caused by pruning the feed-forward network (FFN) layer, we introduce a linear calibration method to reconstruct the residual errors of pruned layers using low-rank matrices. By leveraging singular value decomposition (SVD) on the solution of the least-squares problem, these matrices are obtained without requiring retraining. Extensive experiments show that the proposed Olica is efficient in terms of data usage, GPU memory, and running time, while delivering superior performance across multiple benchmarks.
Deep Transfer Learning: Model Framework and Error Analysis
Oct 12, 2024Abstract:This paper presents a framework for deep transfer learning, which aims to leverage information from multi-domain upstream data with a large number of samples $n$ to a single-domain downstream task with a considerably smaller number of samples $m$, where $m \ll n$, in order to enhance performance on downstream task. Our framework has several intriguing features. First, it allows the existence of both shared and specific features among multi-domain data and provides a framework for automatic identification, achieving precise transfer and utilization of information. Second, our model framework explicitly indicates the upstream features that contribute to downstream tasks, establishing a relationship between upstream domains and downstream tasks, thereby enhancing interpretability. Error analysis demonstrates that the transfer under our framework can significantly improve the convergence rate for learning Lipschitz functions in downstream supervised tasks, reducing it from $\tilde{O}(m^{-\frac{1}{2(d+2)}}+n^{-\frac{1}{2(d+2)}})$ ("no transfer") to $\tilde{O}(m^{-\frac{1}{2(d^*+3)}} + n^{-\frac{1}{2(d+2)}})$ ("partial transfer"), and even to $\tilde{O}(m^{-1/2}+n^{-\frac{1}{2(d+2)}})$ ("complete transfer"), where $d^* \ll d$ and $d$ is the dimension of the observed data. Our theoretical findings are substantiated by empirical experiments conducted on image classification datasets, along with a regression dataset.
Unsupervised Transfer Learning via Adversarial Contrastive Training
Aug 16, 2024Abstract:Learning a data representation for downstream supervised learning tasks under unlabeled scenario is both critical and challenging. In this paper, we propose a novel unsupervised transfer learning approach using adversarial contrastive training (ACT). Our experimental results demonstrate outstanding classification accuracy with both fine-tuned linear probe and K-NN protocol across various datasets, showing competitiveness with existing state-of-the-art self-supervised learning methods. Moreover, we provide an end-to-end theoretical guarantee for downstream classification tasks in a misspecified, over-parameterized setting, highlighting how a large amount of unlabeled data contributes to prediction accuracy. Our theoretical findings suggest that the testing error of downstream tasks depends solely on the efficiency of data augmentation used in ACT when the unlabeled sample size is sufficiently large. This offers a theoretical understanding of learning downstream tasks with a small sample size.
Generative adversarial learning with optimal input dimension and its adaptive generator architecture
May 06, 2024Abstract:We investigate the impact of the input dimension on the generalization error in generative adversarial networks (GANs). In particular, we first provide both theoretical and practical evidence to validate the existence of an optimal input dimension (OID) that minimizes the generalization error. Then, to identify the OID, we introduce a novel framework called generalized GANs (G-GANs), which includes existing GANs as a special case. By incorporating the group penalty and the architecture penalty developed in the paper, G-GANs have several intriguing features. First, our framework offers adaptive dimensionality reduction from the initial dimension to a dimension necessary for generating the target distribution. Second, this reduction in dimensionality also shrinks the required size of the generator network architecture, which is automatically identified by the proposed architecture penalty. Both reductions in dimensionality and the generator network significantly improve the stability and the accuracy of the estimation and prediction. Theoretical support for the consistent selection of the input dimension and the generator network is provided. Third, the proposed algorithm involves an end-to-end training process, and the algorithm allows for dynamic adjustments between the input dimension and the generator network during training, further enhancing the overall performance of G-GANs. Extensive experiments conducted with simulated and benchmark data demonstrate the superior performance of G-GANs. In particular, compared to that of off-the-shelf methods, G-GANs achieves an average improvement of 45.68% in the CT slice dataset, 43.22% in the MNIST dataset and 46.94% in the FashionMNIST dataset in terms of the maximum mean discrepancy or Frechet inception distance. Moreover, the features generated based on the input dimensions identified by G-GANs align with visually significant features.
Latent Schr{ö}dinger Bridge Diffusion Model for Generative Learning
Apr 20, 2024Abstract:This paper aims to conduct a comprehensive theoretical analysis of current diffusion models. We introduce a novel generative learning methodology utilizing the Schr{\"o}dinger bridge diffusion model in latent space as the framework for theoretical exploration in this domain. Our approach commences with the pre-training of an encoder-decoder architecture using data originating from a distribution that may diverge from the target distribution, thus facilitating the accommodation of a large sample size through the utilization of pre-existing large-scale models. Subsequently, we develop a diffusion model within the latent space utilizing the Schr{\"o}dinger bridge framework. Our theoretical analysis encompasses the establishment of end-to-end error analysis for learning distributions via the latent Schr{\"o}dinger bridge diffusion model. Specifically, we control the second-order Wasserstein distance between the generated distribution and the target distribution. Furthermore, our obtained convergence rates effectively mitigate the curse of dimensionality, offering robust theoretical support for prevailing diffusion models.
Covariance-Insured Screening
May 17, 2018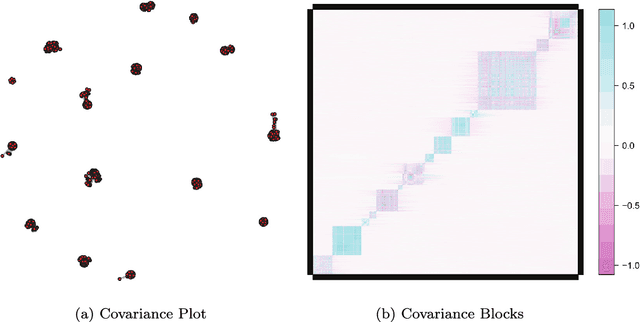
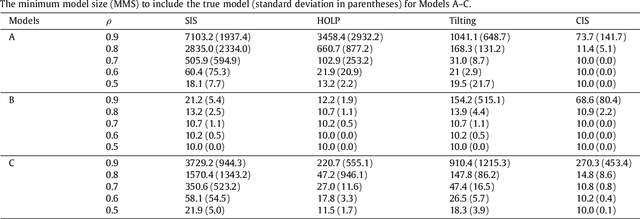
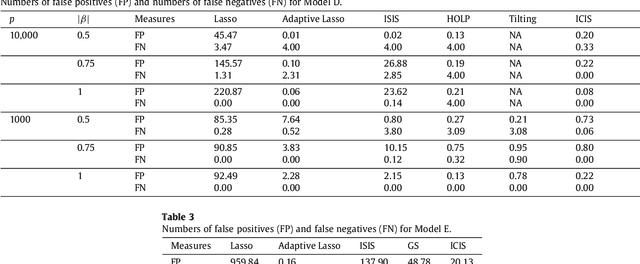
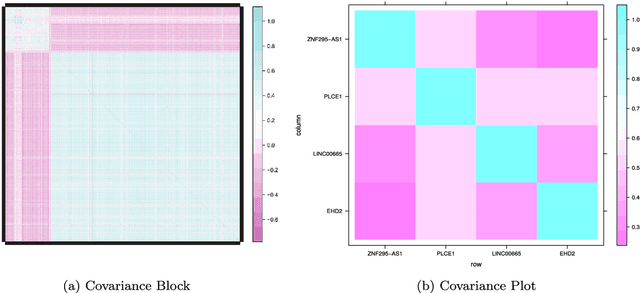
Abstract:Modern bio-technologies have produced a vast amount of high-throughput data with the number of predictors far greater than the sample size. In order to identify more novel biomarkers and understand biological mechanisms, it is vital to detect signals weakly associated with outcomes among ultrahigh-dimensional predictors. However, existing screening methods, which typically ignore correlation information, are likely to miss these weak signals. By incorporating the inter-feature dependence, we propose a covariance-insured screening methodology to identify predictors that are jointly informative but only marginally weakly associated with outcomes. The validity of the method is examined via extensive simulations and real data studies for selecting potential genetic factors related to the onset of cancer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge