Iterative Reweighted Framework Based Algorithms for Sparse Linear Regression with Generalized Elastic Net Penalty

The elastic net penalty is frequently employed in high-dimensional statistics for parameter regression and variable selection. It is particularly beneficial compared to lasso when the number of predictors greatly surpasses the number of observations. However, empirical evidence has shown that the $\ell_q$-norm penalty (where $0 < q < 1$) often provides better regression compared to the $\ell_1$-norm penalty, demonstrating enhanced robustness in various scenarios. In this paper, we explore a generalized elastic net model that employs a $\ell_r$-norm (where $r \geq 1$) in loss function to accommodate various types of noise, and employs a $\ell_q$-norm (where $0 < q < 1$) to replace the $\ell_1$-norm in elastic net penalty. Theoretically, we establish the computable lower bounds for the nonzero entries of the generalized first-order stationary points of the proposed generalized elastic net model. For implementation, we develop two efficient algorithms based on the locally Lipschitz continuous $\epsilon$-approximation to $\ell_q$-norm. The first algorithm employs an alternating direction method of multipliers (ADMM), while the second utilizes a proximal majorization-minimization method (PMM), where the subproblems are addressed using the semismooth Newton method (SNN). We also perform extensive numerical experiments with both simulated and real data, showing that both algorithms demonstrate superior performance. Notably, the PMM-SSN is efficient than ADMM, even though the latter provides a simpler implementation.

A Data-Driven Line Search Rule for Support Recovery in High-dimensional Data Analysis

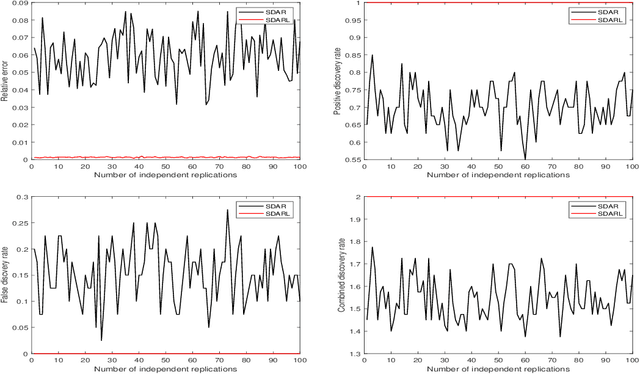
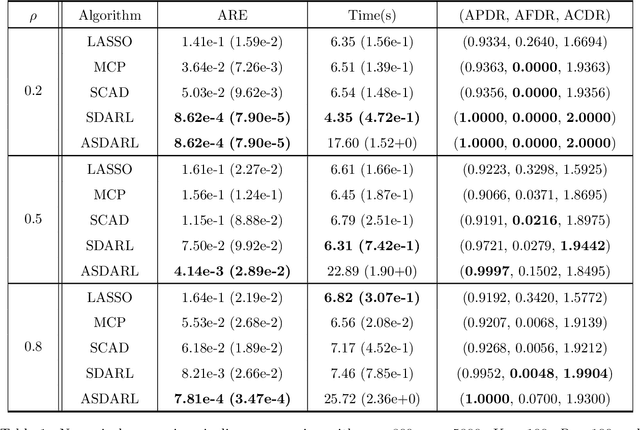
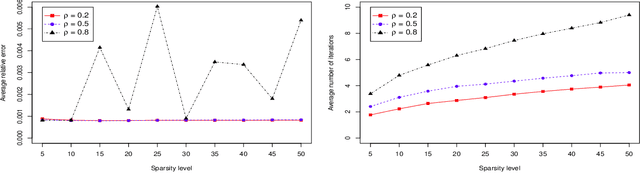
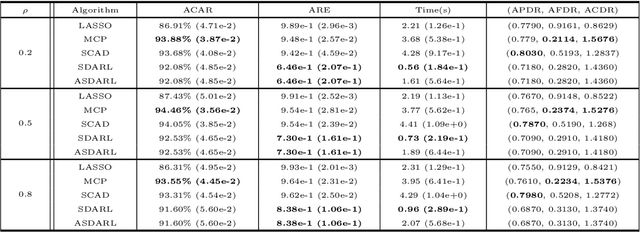
In this work, we consider the algorithm to the (nonlinear) regression problems with $\ell_0$ penalty. The existing algorithms for $\ell_0$ based optimization problem are often carried out with a fixed step size, and the selection of an appropriate step size depends on the restricted strong convexity and smoothness for the loss function, hence it is difficult to compute in practical calculation. In sprite of the ideas of support detection and root finding \cite{HJK2020}, we proposes a novel and efficient data-driven line search rule to adaptively determine the appropriate step size. We prove the $\ell_2$ error bound to the proposed algorithm without much restrictions for the cost functional. A large number of numerical comparisons with state-of-the-art algorithms in linear and logistic regression problems show the stability, effectiveness and superiority of the proposed algorithms.