Cycle Pixel Difference Network for Crisp Edge Detection

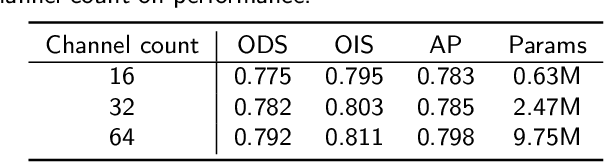
Edge detection, as a fundamental task in computer vision, has garnered increasing attention. The advent of deep learning has significantly advanced this field. However, recent deep learning-based methods which rely on large-scale pre-trained weights cannot be trained from scratch, with very limited research addressing this issue. This paper proposes a novel cycle pixel difference convolution (CPDC), which effectively integrates image gradient information with modern convolution operations. Based on the CPDC, we develop a U-shape encoder-decoder model named CPD-Net, which is a purely end-to-end network. Additionally, to address the issue of edge thickness produced by most existing methods, we construct a multi-scale information enhancement module (MSEM) to enhance the discriminative ability of the model, thereby generating crisp and clean contour maps. Comprehensive experiments conducted on three standard benchmarks demonstrate that our method achieves competitive performance on the BSDS500 dataset (ODS=0.813), NYUD-V2 (ODS=0.760), and BIPED dataset (ODS=0.898). Our approach provides a novel perspective for addressing these challenges in edge detection.

Learning to utilize gradient information for crisp edge detection

Edge detection is a fundamental task in computer vision and it has made great progress under the development of deep convolutional neural networks (DCNNs), some of them have achieved a beyond human-level performance. However, recent top-performing edge detection methods tend to generate thick and blurred edge lines. In this work, we propose an effective method to solve this problem. Our approach consists of a lightweight pre-trained backbone, multi-scale contextual enhancement module aggregating gradient information (MCGI), boundary correction module (BCM), and boundary refinement module (BRM). In addition to this, we construct a novel hybrid loss function based on the Tversky index for solving the issue of imbalanced pixel distribution. We test our method on three standard benchmarks and the experiment results illustrate that our method improves the visual effect of edge maps and achieves a top performance among several state-of-the-art methods on the BSDS500 dataset (ODS F-score in standard evaluation is 0.829, in crispness evaluation is 0.720), NYUD-V2 dataset (ODS F-score in standard evaluation is 0.768, in crispness evaluation is \textbf{0.546}), and BIPED dataset (ODS F-score in standard evaluation is 0.903).

An Efficient Construction Method Based on Partial Distance of Polar Codes with Reed-Solomon Kernel

Polar codes with Reed-Solomon (RS) kernel have great potential in next-generation communication systems due to their high polarization rate. In this paper, we study the polarization characteristics of RS polar codes and propose two types of partial orders (POs) for the synthesized channels, which are supported by validity proofs. By combining these partial orders, a Partial Distance-based Polarization Weight (PDPW) construction method is presented. The proposed method achieves comparable performance to Monte-Carlo simulations while requiring lower complexity. Additionally, a Minimum Polarization Weight Puncturing (MPWP) scheme for rate-matching is proposed to enhance its practical applicability in communication systems. Simulation results demonstrate that the RS polar codes based on the proposed PDPW construction outperform the 3rd Generation Partnership Project (3GPP) NR polar codes in terms of standard code performance and rate-matching performance.

An efficient real-time target tracking algorithm using adaptive feature fusion

Visual-based target tracking is easily influenced by multiple factors, such as background clutter, targets fast-moving, illumination variation, object shape change, occlusion, etc. These factors influence the tracking accuracy of a target tracking task. To address this issue, an efficient real-time target tracking method based on a low-dimension adaptive feature fusion is proposed to allow us the simultaneous implementation of the high-accuracy and real-time target tracking. First, the adaptive fusion of a histogram of oriented gradient (HOG) feature and color feature is utilized to improve the tracking accuracy. Second, a convolution dimension reduction method applies to the fusion between the HOG feature and color feature to reduce the over-fitting caused by their high-dimension fusions. Third, an average correlation energy estimation method is used to extract the relative confidence adaptive coefficients to ensure tracking accuracy. We experimentally confirm the proposed method on an OTB100 data set. Compared with nine popular target tracking algorithms, the proposed algorithm gains the highest tracking accuracy and success tracking rate. Compared with the traditional Sum of Template and Pixel-wise LEarners (STAPLE) algorithm, the proposed algorithm can obtain a higher success rate and accuracy, improving by 0.023 and 0.019, respectively. The experimental results also demonstrate that the proposed algorithm can reach the real-time target tracking with 50 fps. The proposed method paves a more promising way for real-time target tracking tasks under a complex environment, such as appearance deformation, illumination change, motion blur, background, similarity, scale change, and occlusion.

Convergence Analysis of Schr{ö}dinger-F{ö}llmer Sampler without Convexity

Schr\"{o}dinger-F\"{o}llmer sampler (SFS) is a novel and efficient approach for sampling from possibly unnormalized distributions without ergodicity. SFS is based on the Euler-Maruyama discretization of Schr\"{o}dinger-F\"{o}llmer diffusion process $$\mathrm{d} X_{t}=-\nabla U\left(X_t, t\right) \mathrm{d} t+\mathrm{d} B_{t}, \quad t \in[0,1],\quad X_0=0$$ on the unit interval, which transports the degenerate distribution at time zero to the target distribution at time one. In \cite{sfs21}, the consistency of SFS is established under a restricted assumption that %the drift term $b(x,t)$ the potential $U(x,t)$ is uniformly (on $t$) strongly %concave convex (on $x$). In this paper we provide a nonasymptotic error bound of SFS in Wasserstein distance under some smooth and bounded conditions on the density ratio of the target distribution over the standard normal distribution, but without requiring the strongly convexity of the potential.

On Newton Screening

Screening and working set techniques are important approaches to reducing the size of an optimization problem. They have been widely used in accelerating first-order methods for solving large-scale sparse learning problems. In this paper, we develop a new screening method called Newton screening (NS) which is a generalized Newton method with a built-in screening mechanism. We derive an equivalent KKT system for the Lasso and utilize a generalized Newton method to solve the KKT equations. Based on this KKT system, a built-in working set with a relatively small size is first determined using the sum of primal and dual variables generated from the previous iteration, then the primal variable is updated by solving a least-squares problem on the working set and the dual variable updated based on a closed-form expression. Moreover, we consider a sequential version of Newton screening (SNS) with a warm-start strategy. We show that NS possesses an optimal convergence property in the sense that it achieves one-step local convergence. Under certain regularity conditions on the feature matrix, we show that SNS hits a solution with the same signs as the underlying true target and achieves a sharp estimation error bound with high probability. Simulation studies and real data analysis support our theoretical results and demonstrate that SNS is faster and more accurate than several state-of-the-art methods in our comparative studies.

A Support Detection and Root Finding Approach for Learning High-dimensional Generalized Linear Models

Feature selection is important for modeling high-dimensional data, where the number of variables can be much larger than the sample size. In this paper, we develop a support detection and root finding procedure to learn the high dimensional sparse generalized linear models and denote this method by GSDAR. Based on the KKT condition for $\ell_0$-penalized maximum likelihood estimations, GSDAR generates a sequence of estimators iteratively. Under some restricted invertibility conditions on the maximum likelihood function and sparsity assumption on the target coefficients, the errors of the proposed estimate decays exponentially to the optimal order. Moreover, the oracle estimator can be recovered if the target signal is stronger than the detectable level. We conduct simulations and real data analysis to illustrate the advantages of our proposed method over several existing methods, including Lasso and MCP.