Modeling Randomly Walking Volatility with Chained Gamma Distributions

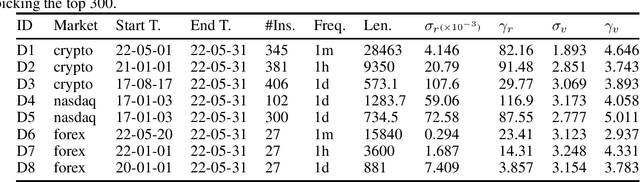
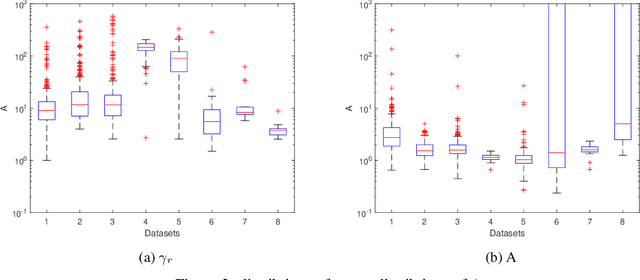
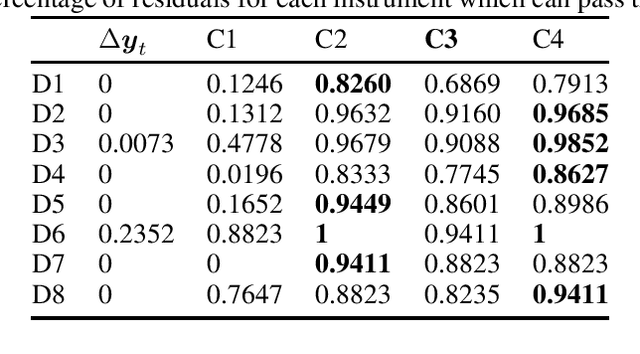
Volatility clustering is a common phenomenon in financial time series. Typically, linear models are used to describe the temporal autocorrelation of the (logarithmic) variance of returns. Considering the difficulty in estimation of this model, we construct a Dynamic Bayesian Network, which utilizes the conjugate prior relation of normal-gamma and gamma-gamma, so that at each node, its posterior form locally remains unchanged. This makes it possible to quickly find approximate solutions using variational methods. Furthermore, we ensure that the volatility expressed by the model is an independent incremental process after inserting dummy gamma nodes between adjacent time steps. We have found that, this model has two advantages: 1) It can be proved that it can express heavier tails than Gaussians, i.e., have positive excess kurtosis, compared to popular linear models. 2) If the variational inference(VI) is used for state estimation, it runs much faster than Monte Carlo(MC) methods, since the calculation of the posterior uses only basic arithmetic operations. And, its convergence process is deterministic. We tested the model, named Gam-Chain, using recent Crypto, Nasdaq, and Forex records of varying resolutions. The results show that: 1) In the same case of using MC, this model can achieve comparable state estimation results with the regular lognormal chain. 2) In the case of only using VI, this model can obtain accuracy that are slightly worse than MC, but still acceptable in practice; 3) Only using VI, the running time of Gam-Chain, under the most conservative settings, can be reduced to below 20% of that based on the lognormal chain via MC.

Convergence Analysis of Schr{ö}dinger-F{ö}llmer Sampler without Convexity

Schr\"{o}dinger-F\"{o}llmer sampler (SFS) is a novel and efficient approach for sampling from possibly unnormalized distributions without ergodicity. SFS is based on the Euler-Maruyama discretization of Schr\"{o}dinger-F\"{o}llmer diffusion process $$\mathrm{d} X_{t}=-\nabla U\left(X_t, t\right) \mathrm{d} t+\mathrm{d} B_{t}, \quad t \in[0,1],\quad X_0=0$$ on the unit interval, which transports the degenerate distribution at time zero to the target distribution at time one. In \cite{sfs21}, the consistency of SFS is established under a restricted assumption that %the drift term $b(x,t)$ the potential $U(x,t)$ is uniformly (on $t$) strongly %concave convex (on $x$). In this paper we provide a nonasymptotic error bound of SFS in Wasserstein distance under some smooth and bounded conditions on the density ratio of the target distribution over the standard normal distribution, but without requiring the strongly convexity of the potential.