Clustering Causal Additive Noise Models

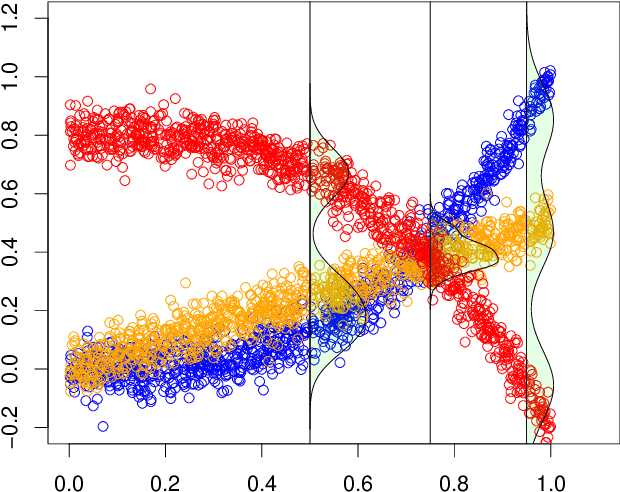
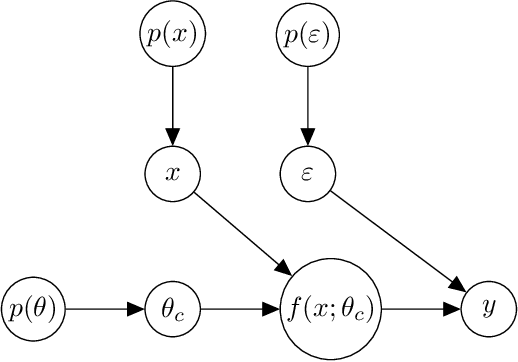
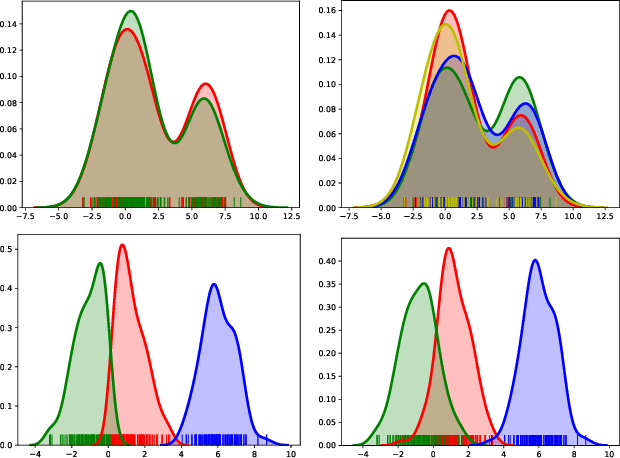
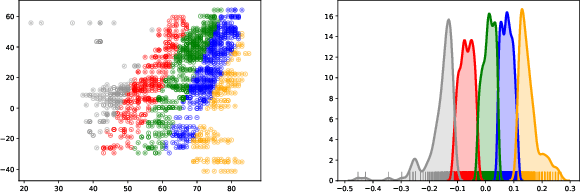
Additive noise models are commonly used to infer the causal direction for a given set of observed data. Most causal models assume a single homogeneous population. However, observations may be collected under different conditions in practice. Such data often require models that can accommodate possible heterogeneity caused by different conditions under which data have been collected. We propose a clustering algorithm inspired by the $k$-means algorithm, but with unknown $k$. Using the proposed algorithm, both the labels and the number of components are estimated from the collected data. The estimated labels are used to adjust the causal direction test statistic. The adjustment significantly improves the performance of the test statistic in identifying the correct causal direction.