Causal Coordinated Concurrent Reinforcement Learning

In this work, we propose a novel algorithmic framework for data sharing and coordinated exploration for the purpose of learning more data-efficient and better performing policies under a concurrent reinforcement learning (CRL) setting. In contrast to other work which make the assumption that all agents act under identical environments, we relax this restriction and instead consider the formulation where each agent acts within an environment which shares a global structure but also exhibits individual variations. Our algorithm leverages a causal inference algorithm in the form of Additive Noise Model - Mixture Model (ANM-MM) in extracting model parameters governing individual differentials via independence enforcement. We propose a new data sharing scheme based on a similarity measure of the extracted model parameters and demonstrate superior learning speeds on a set of autoregressive, pendulum and cart-pole swing-up tasks and finally, we show the effectiveness of diverse action selection between common agents under a sparse reward setting. To the best of our knowledge, this is the first work in considering non-identical environments in CRL and one of the few works which seek to integrate causal inference with reinforcement learning (RL).

Causal Discovery by Kernel Deviance Measures with Heterogeneous Transforms

The discovery of causal relationships in a set of random variables is a fundamental objective of science and has also recently been argued as being an essential component towards real machine intelligence. One class of causal discovery techniques are founded based on the argument that there are inherent structural asymmetries between the causal and anti-causal direction which could be leveraged in determining the direction of causation. To go about capturing these discrepancies between cause and effect remains to be a challenge and many current state-of-the-art algorithms propose to compare the norms of the kernel mean embeddings of the conditional distributions. In this work, we argue that such approaches based on RKHS embeddings are insufficient in capturing principal markers of cause-effect asymmetry involving higher-order structural variabilities of the conditional distributions. We propose Kernel Intrinsic Invariance Measure with Heterogeneous Transform (KIIM-HT) which introduces a novel score measure based on heterogeneous transformation of RKHS embeddings to extract relevant higher-order moments of the conditional densities for causal discovery. Inference is made via comparing the score of each hypothetical cause-effect direction. Tests and comparisons on a synthetic dataset, a two-dimensional synthetic dataset and the real-world benchmark dataset T\"ubingen Cause-Effect Pairs verify our approach. In addition, we conduct a sensitivity analysis to the regularization parameter to faithfully compare previous work to our method and an experiment with trials on varied hyperparameter values to showcase the robustness of our algorithm.

Causal Discovery by Kernel Intrinsic Invariance Measure

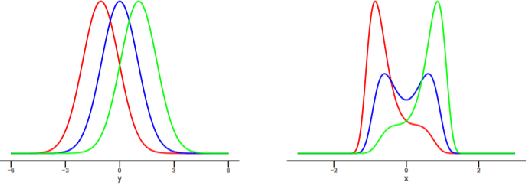
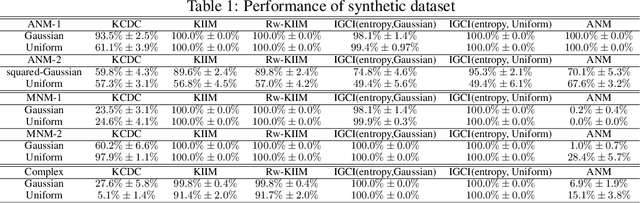
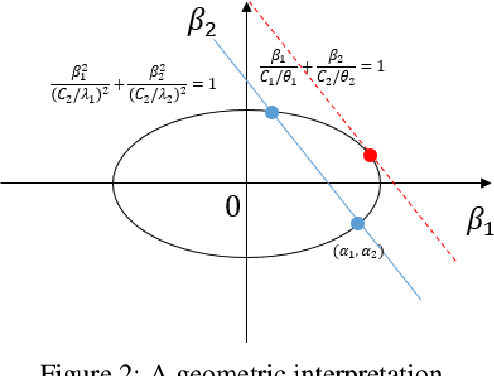
Reasoning based on causality, instead of association has been considered as a key ingredient towards real machine intelligence. However, it is a challenging task to infer causal relationship/structure among variables. In recent years, an Independent Mechanism (IM) principle was proposed, stating that the mechanism generating the cause and the one mapping the cause to the effect are independent. As the conjecture, it is argued that in the causal direction, the conditional distributions instantiated at different value of the conditioning variable have less variation than the anti-causal direction. Existing state-of-the-arts simply compare the variance of the RKHS mean embedding norms of these conditional distributions. In this paper, we prove that this norm-based approach sacrifices important information of the original conditional distributions. We propose a Kernel Intrinsic Invariance Measure (KIIM) to capture higher order statistics corresponding to the shapes of the density functions. We show our algorithm can be reduced to an eigen-decomposition task on a kernel matrix measuring intrinsic deviance/invariance. Causal directions can then be inferred by comparing the KIIM scores of two hypothetic directions. Experiments on synthetic and real data are conducted to show the advantages of our methods over existing solutions.